Hoop Stress Thin-wall Section Formula |
||
|
\( \sigma_h \;=\; \dfrac{ p \cdot r }{ t } \) (Hoop Stress Thin-wall Section) \( p \;=\; \dfrac{ \sigma_h \cdot t }{ r } \) \( r \;=\; \dfrac{ \sigma_h \cdot t }{ p } \) \( t \;=\; \dfrac{ p \cdot r }{ \sigma_h } \) |
||
| Symbol | English | Metric |
| \( \sigma_h \) (Greek symbol sigma) = Spherical Hoop Stress | \(lbf\;/\;in^2\) | \(Pa\) |
| \( p \) = Pressure Under Consideration | \(lbf\;/\;in^2\) | \(Pa\) |
| \( r \) = Radius to Point of Intrest | \( in \) | \( mm \) |
| \( t \) = Wall Thickness | \( in \) | \( mm \) |
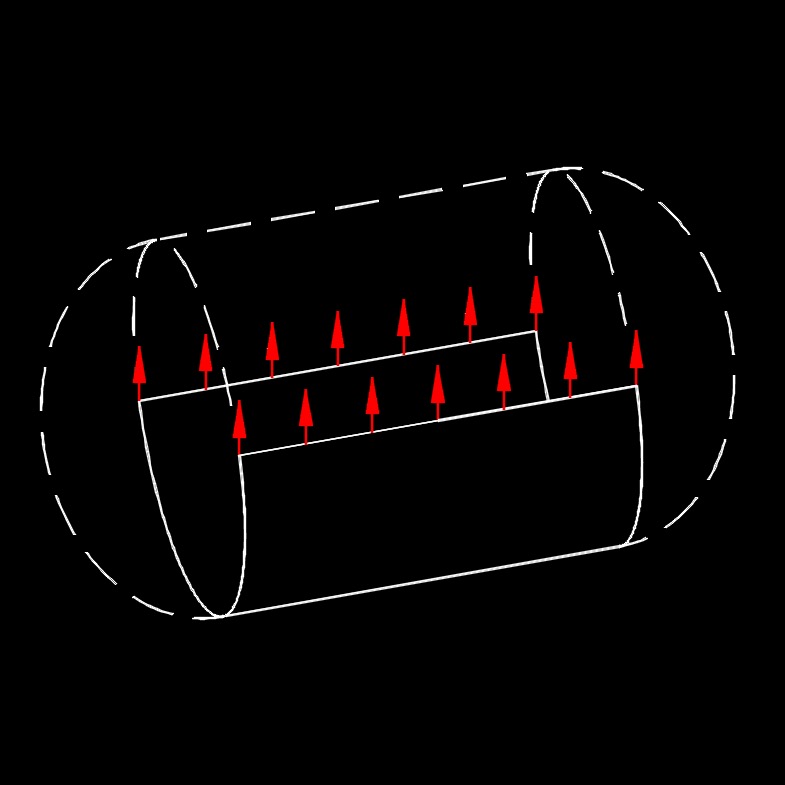Hoop stress in a thin-wall section refers to the stress that acts circumferentially or tangentially around the circumference of a cylindrical or spherical structure with a relatively thin wall compared to its diameter or radius. It is an important concept in engineering and mechanics, particularly in the analysis of pressure vessels, pipes, and other structures that involve cylindrical or spherical shapes.
Hoop Stress in a Thin-wall Section Key Characteristics
- Hoop stress is a result of the internal pressure or fluid pressure inside the structure trying to push the walls outward. It is the primary stress component in this scenario.
- The formula assumes that the material of the structure behaves elastically. If the material is not elastic, more complex stress analysis is required.
- Thin-walled structures are typically designed to ensure that the hoop stress does not exceed the material's allowable stress or yield strength to prevent failure due to excessive pressure.
- In contrast to hoop stress, there is also longitudinal stress (axial stress) in such structures, which acts along the length of the cylinder or sphere. The calculation for longitudinal stress is different from that of hoop stress.
- Thin-walled structures are commonly found in applications like pressure vessels, pipelines, and containers used in various industries, including chemical processing, oil and gas, and aerospace.
Understanding hoop stress in thin-walled sections is crucial for designing safe and reliable structures that can withstand internal pressure without rupturing or experiencing plastic deformation. Engineers and designers use these stress calculations to determine the appropriate wall thickness and material selection for such structures to meet safety and performance requirements.
