Passing Sight Distance Formula |
||
| \( PSD \;=\; d_1 + d_2 + d_3 + d_4 \) | ||
| Symbol | English | Metric |
| \( PSD \) = passing sight distance | \(ft\) | \(m\) |
| \( d_1 \) = initial maneuver distance | \(ft\) | \(m\) |
| \( d_2 \) = distance while passing vehicle occupies left lane | \(ft\) | \(m\) |
| \( d_3 \) = clearance length | \(ft\) | \(m\) |
| \( d_4 \) = distance traversed by opposing vehicle | \(ft\) | \(m\) |
Passing sight distance, abbreviated as PSD, is another important concept in transportation engineering, particularly for designing roads and highways where vehicles need to safely overtake or pass slower-moving vehicles. It refers to the distance required for a driver to safely pass another vehicle while maintaining a safe margin from oncoming traffic.
Passing Sight Distance Takes into Account Several Factors
Overtaking Vehicle Speed - The speed at which the passing vehicle is traveling.Speed of the Vehicle Being Passed - The speed of the slower-moving vehicle that the passing vehicle is overtaking.
Speed of Oncoming Traffic - The speed of vehicles coming from the opposite direction.
Driver's Perception and Reaction Time - The time it takes for the passing driver to perceive the need to overtake, decide to initiate the passing maneuver, and move into the oncoming lane.
Passing Maneuver Time - The time required for the passing vehicle to move into the oncoming lane, pass the slower vehicle, and return to the original lane.
Passing Clearance - The minimum distance that should be maintained from oncoming traffic to ensure safe passage.
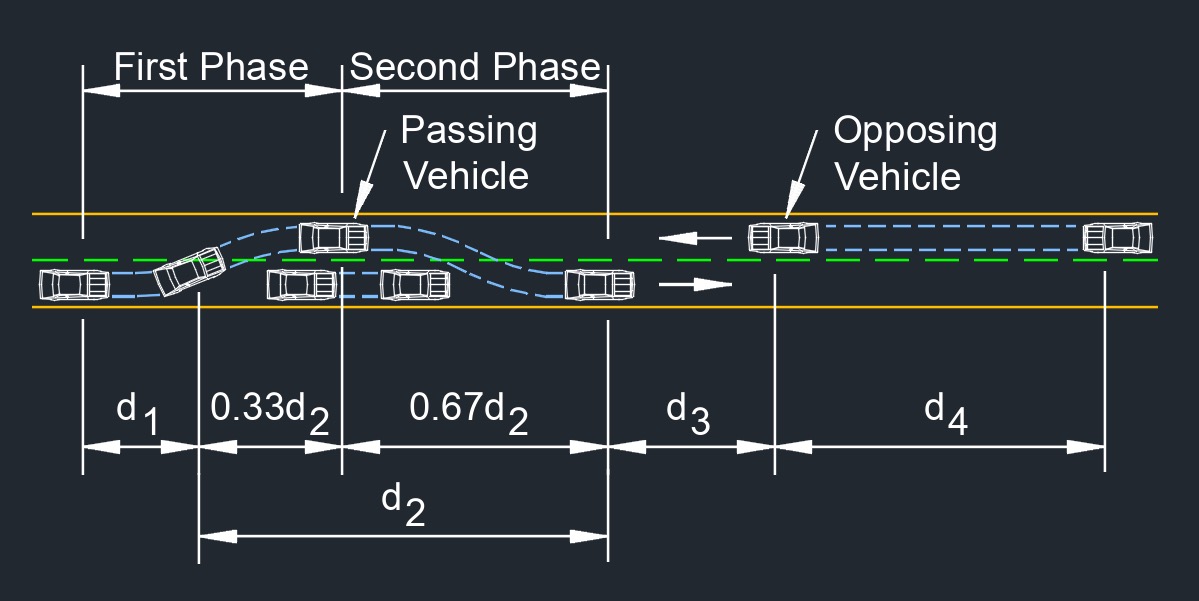
PSD is crucial for designing roads with sufficient lane width, clear zones, and proper visibility to allow safe overtaking maneuvers. Engineers consider factors like road geometry, sightlines, lane markings, and the presence of curves or hills to determine the necessary PSD for different road segments. Just like other sight distance calculations, guidelines and standards provide specific values for PSD based on various factors, including road type, speed limits, and design considerations.
