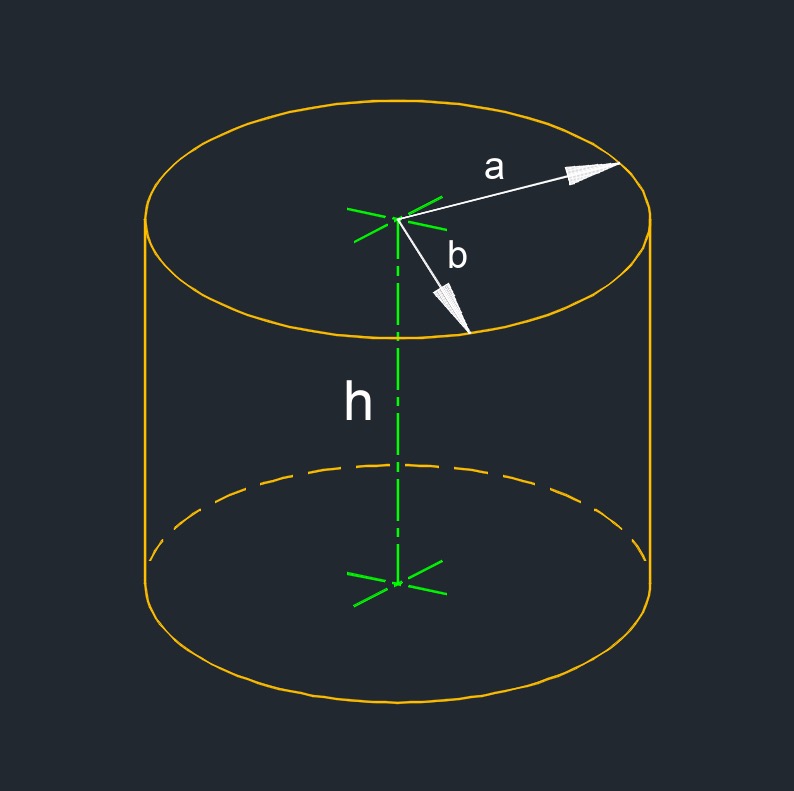
Right Elliptic Cylinder
Lateral Surface Area of a Right Elliptic Cylinder formula |
||
| \( A_l \; \approx \; h \cdot \left( 2 \cdot \pi \cdot \sqrt { \; \dfrac{1}{2} \cdot \left(a^2 + b^2 \right) } \right) \) | ||
| Symbol | English | Metric |
| \( A_l \) = approximate lateral surface area (side) | \( in^2 \) | \( mm^2 \) |
| \( a \) = length semi-major axis | \( in \) | \( mm \) |
| \( b \) = length semi-minor axis | \( in \) | \( mm \) |
| \( h \) = height | \( in \) | \( mm \) |
- Elliptic cylinder (a three-dimensional figure) has a cylinder shape with elliptical ends.
- 2 bases

Surface Area of a Right Elliptic Cylinder formula |
||
| \( A_s \; \approx \; h \cdot \left( 2 \cdot \pi \cdot \sqrt {\; \dfrac{1}{2} \cdot \left(a^2 + b^2 \right) } \right) + 2\cdot \left( \pi \cdot a \cdot b \right) \) | ||
| Symbol | English | Metric |
| \( A_s \) = approximate surface area (bottom, top, side) | \( in^2 \) | \( mm^2 \) |
| \( a \) = length semi-major axis | \( in \) | \( mm \) |
| \( b \) = length semi-minor axis | \( in \) | \( mm \) |
| \( h \) = height | \( in \) | \( mm \) |
Volume of a Right Elliptic Cylinder formula |
||
| \( V \;=\; \pi \cdot a \cdot b \cdot h \) | ||
| Symbol | English | Metric |
| \( V \) = volume | \( in^3 \) | \( mm^3 \) |
| \( a \) = length semi-major axis | \( in \) | \( mm \) |
| \( b \) = length semi-minor axis | \( in \) | \( mm \) |
| \( h \) = height | \( in \) | \( mm \) |