Centrifugal Force by Angular Velocity Formula |
||
|
\( F_c \;=\; m \cdot \omega^2 \cdot r \) (Centrifugal Force by Angular Velocity) \( m \;=\; \dfrac{ F_c }{ \omega^2 \cdot r }\) \( \omega \;=\; \sqrt{ \dfrac{ F_c }{ m \cdot r } } \) \( r \;=\; \dfrac{ F_c }{ m \cdot \omega^2 }\) |
||
| Symbol | English | Metric |
| \( F_c \) = Centrifugal Force | \(lbf\) | \(N\) |
| \( m \) = Mass | \(lbm\) | \(kg\) |
| \( \omega \) (Greek symbol omega) = Angular Velocity | \(deg\;/\;sec\) | \(rad\;/\;s\) |
| \( r \) = Radius from the Origin | \(ft\) | \(m\) |
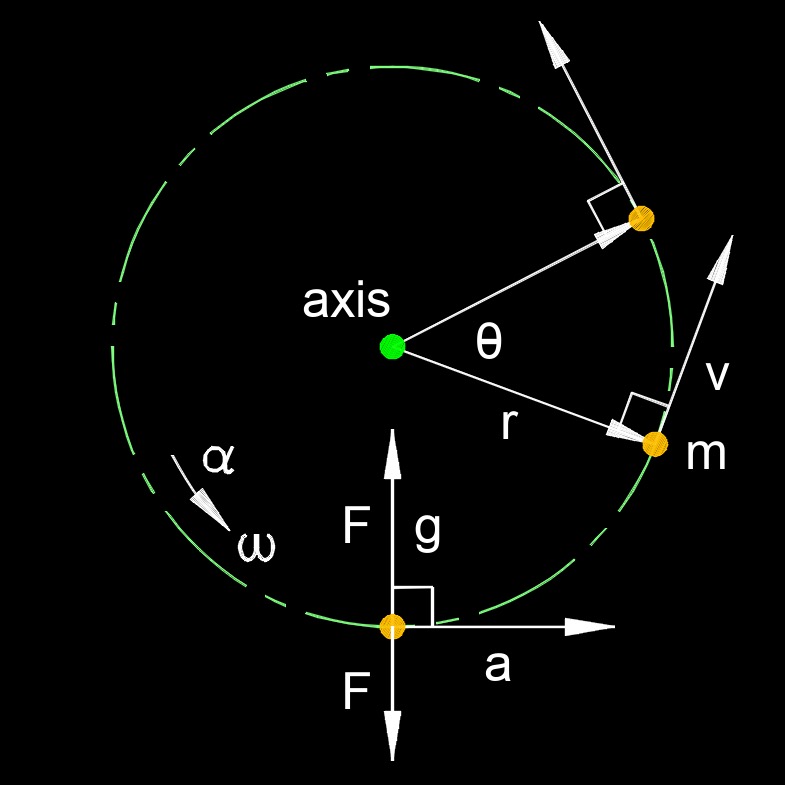 Centrifugal force, abbreviated as \(F_c\) or \(F_{cf}\), is used to describe the apparent force that pushes an object away from the center of rotation when it is in a rotating reference frame. Although often referred to as a force, it is actually a result of inertia and the tendency of objects to resist changes in their motion. When an object travels in a circle, the object always wants to go straight, but the centripetal force keeps the object traveling along an axis of rotation.
Centrifugal force, abbreviated as \(F_c\) or \(F_{cf}\), is used to describe the apparent force that pushes an object away from the center of rotation when it is in a rotating reference frame. Although often referred to as a force, it is actually a result of inertia and the tendency of objects to resist changes in their motion. When an object travels in a circle, the object always wants to go straight, but the centripetal force keeps the object traveling along an axis of rotation.
Centrifugal Force by Tangential Velocity Formula |
||
|
\( F_c \;=\; \dfrac{ m \cdot v_t^2 }{ r }\) (Centrifugal Force by Tangential Velocity) \( m \;=\; \dfrac{ F_c \cdot r }{ v_t^2 }\) \( v_t \;=\; \sqrt{ \dfrac{ F_c \cdot r }{ m } }\) \( r \;=\; \dfrac{ m \cdot v_t^2 }{ F_c }\) |
||
| Symbol | English | Metric |
| \( F_c \) = Centrifugal Force | \(lbf\) | \(N\) |
| \( m \) = Mass | \(lbm\) | \(kg\) |
| \( v_t \) = Tangential Velocity | \(ft\;/\;sec\) | \(m\;/\;sec\) |
| \( r \) = Radius from the Origin | \(ft\) | \(m\) |
Also when an object moves in a circular path, it experiences a centrifugal force that acts outward, away from the center of rotation. This apparent force is perceived from the rotating frame of reference and can give the impression of a real force pushing the object outward. In reality, the object tends to move in a straight line tangent to its circular path due to its inertia, but it is continuously redirected by the inward centripetal force that keeps it on the circular path.
Centrifugal force is often observed in everyday situations, such as when riding a carousel or driving a vehicle around a curved path. In these cases, individuals or objects experience a sensation or tendency to be pushed away from the center of rotation. However, it is important to note that the actual force responsible for keeping objects on a curved path is the centripetal force acting inward towards the center.
From a physics perspective, it is more accurate to refer to centrifugal force as a pseudo-force or an apparent force. It is a useful concept for analyzing motion in a rotating frame of reference, but it does not represent a genuine force acting on an object.

Centrifugal Force in RPM Formula |
||
|
\( F_c \;=\; \dfrac{ 30 }{ pi } \cdot m \cdot RPM^2 \cdot r \) (Centrifugal Force in RPM) \( m \;=\; \dfrac{ \pi \cdot F_c }{ 30 \cdot RPM^2 \cdot r } \) \( RPM \;=\; \sqrt{ \dfrac{ \pi \cdot F_c}{ 30 \cdot m \cdot r } }\) \( r \;=\; \dfrac{ \pi \cdot F_c }{ 30 \cdot m \cdot RPM^2 } \) |
||
| Symbol | English | Metric |
| \( F_c \) = Centrifugal Force | \(lbf\) | \(N\) |
| \( \pi \) = Pi | \(3.141 592 653 ...\) | \(3.141 592 653 ...\) |
| \( m \) = Mass | \(lbm\) | \(kg\) |
| \( RPM \) = Revolutions per Minute | \(rev\;/\;min\) | \(rev\;/\;min\) |
| \( r \) = Radius from the Origin | \(ft\) | \(m\) |