Collinear Force Formula |
||
| \( F_{net} \;=\; F_1 \;+ F_2 \;+ ... + \;F_n \) | ||
| Symbol | English | Metric |
| \( F_{net} \) = Resulting Force Acting on Object | \(lbf\) | \(N\) |
| \( F_1 + F_2 \;+ ... + \;F_n \) = Collinear Forces Acting on Object | \(lbf\) | \(N\) |
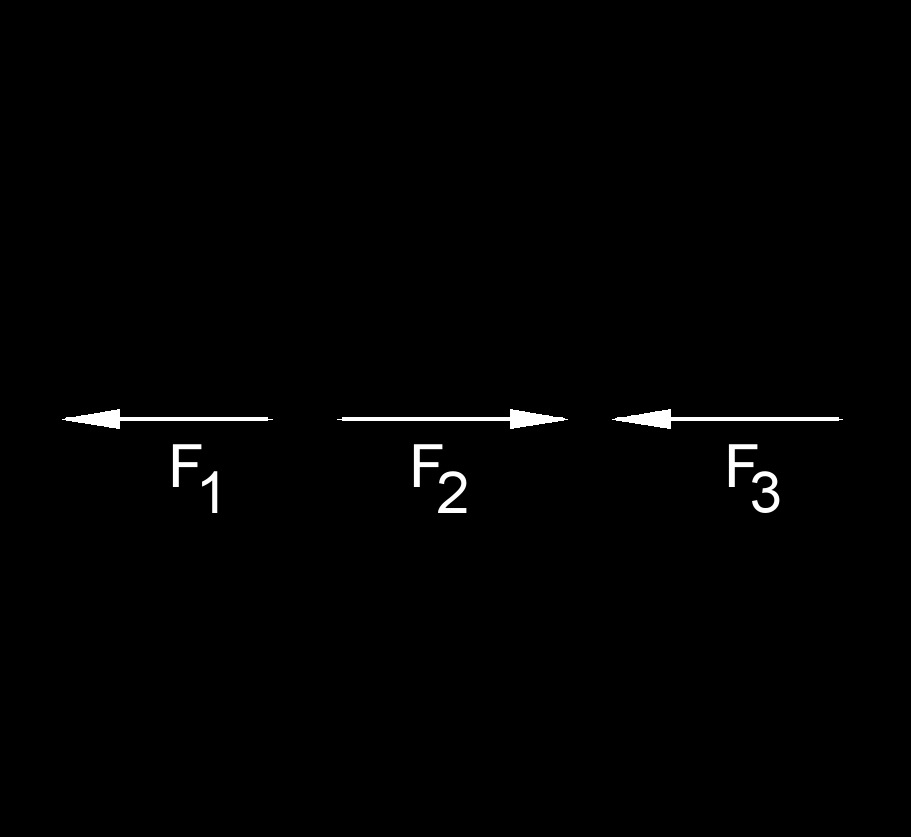Collinear forces are a set of forces that act along the same straight line. These forces have the same or parallel directions, and their effects can be combined by simple vector addition. When multiple forces are collinear, you can add or subtract them by considering their magnitudes and directions along the common line of action. All the forces share the same line of action. The collinear forces are \(F_1\), \(F_2\), and \(F_n\). Collinear forces are relatively straightforward to work with because their vector addition is simplified due to their alignment. You can represent each force as a vector with a magnitude and direction, and then add or subtract these vectors to find the resultant force.
Collinear forces are a concept in mechanics and are often encountered in various real-world situations, such as tension in a rope, compression in a column, or the forces acting on an object along a straight path. Understanding how to analyze and calculate collinear forces is essential in solving problems related to equilibrium, motion, and structural analysis.
