Length of Crest Vertical Curve for Stopping Sight Distance

The Length of Crest Vertical Curve for Stopping Sight Distance is the distance required for a crest vertical curve on a roadway to provide adequate stopping sight distance for drivers.  A crest vertical curve is a design element used on roads that have hills or changes in grade.  It is specifically designed to ensure that drivers approaching the crest of a hill have enough visibility to see any potential hazards, such as vehicles or obstacles, on the other side of the hill and have sufficient distance to stop if necessary.

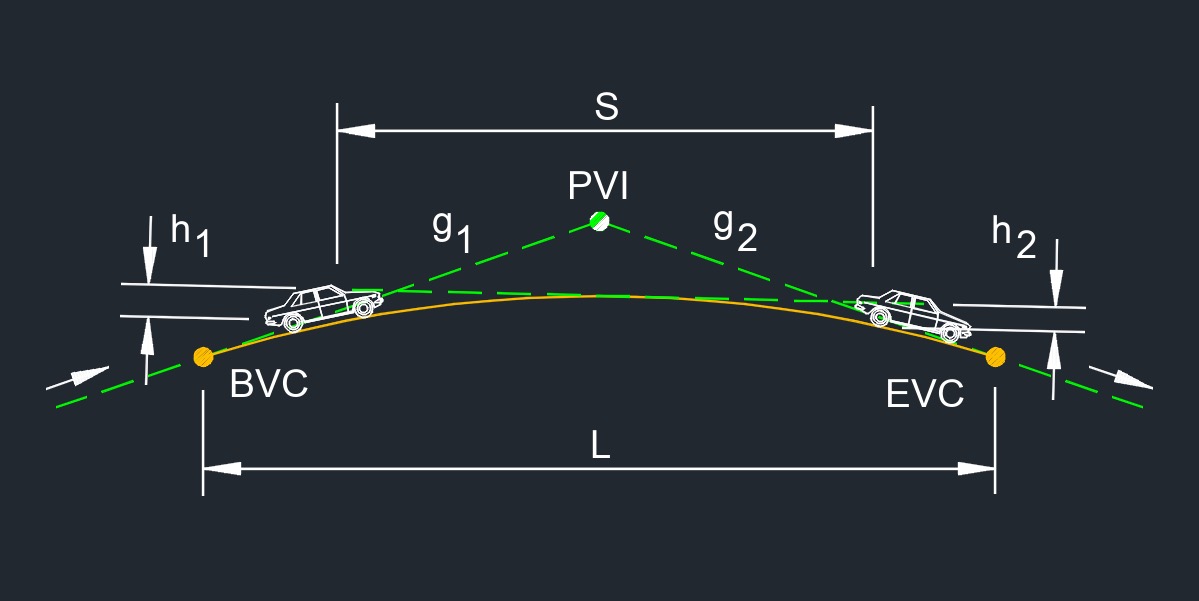
The Stopping Sight Distance for a crest vertical curve includes the distance required for a driver to perceive a hazard on the road ahead, react to it, and bring their vehicle to a complete stop.  It takes into account the driver's perception and reaction time, as well as the braking distance.

Length of Crest Vertical Curve for Stopping Sight Distance is calculated based on factors

• Design Speed  -  The speed at which vehicles are expected to travel on the road.
• Grade of the Hill  -  The slope or incline of the hill.
• Height of the Driver's Eye  -  The height at which a driver's eyes are positioned above the road surface.
• Height of the Object Being Viewed  -  The height of the object or hazard that needs to be visible to the driver.

The formula for calculating the Length of Crest Vertical Curve for Stopping Sight Distance involves determining the distance required for a driver to stop under the given conditions.  This calculation ensures that the driver has a clear line of sight over the hill and enough distance to react and stop safely.  Road designers and engineers use this calculation to determine the appropriate length of crest vertical curves, helping to ensure road safety and prevent accidents related to limited visibility on hills and curves.  Guidelines and standards set by transportation agencies provide specific recommendations for these design elements based on road type, design speed, and other relevant factors.

 

Length of Crest vertical curve for stopping Sight Distance formulas
\( L =   A \; S^2  \;/\; 100 \; ( \sqrt{ 2\;h_1 } + \sqrt{ 2\;h_2 } \; )^2  \)     (\(S \;<\; L\)) (crest vertical curve) \( L = 2 \; S - [\; 200 \; ( \sqrt{ h_1 } + \sqrt{ h_2 }\; )^2 \;/\; A\; ]  \)     (\(S \;>\; L\)) (crest vertical curve) \( L =  A \; S^2 \;/\; 2158 \)     (\(S \;<\; L\)) (when the height of eye and the height of object are 3.5' and 2' respectively, as uesd for breaking distance) (crest vertical curve) \( L = 2 \; S - ( 2158 \;/\; A ) \)     (\(S \;>\; L\)) (when the height of eye and the height of object are 3.5' and 2' respectively, as uesd for breaking distance) (crest vertical curve) \( L = K \; A  \)     (crest vertical curve)
Symbol	English	Metric
\( L \) = length of vertical curve	\(ft\)	\(m\)
\( A \) = algebric difference in grade (%)	\(dimensionless\)
\( h_1 \) = height of drivers' eyes above the roadway surface	\(ft\)	\(m\)
\( h_2 \) = height of object above the roadway surface	\(ft\)	\(m\)
\( K \) = K value	\(ft\)	\(m\)
\( S \) = sight distance for stopping or passing	\(ft\)	\(m\)