Capacitor
Capacitor Circuit Formula |
||
|
\(C \;=\; \dfrac{ Q }{ V }\) (Capacitor) \( Q \;=\; C \cdot V \) \( V \;=\; \dfrac{ Q }{ C }\) |
||
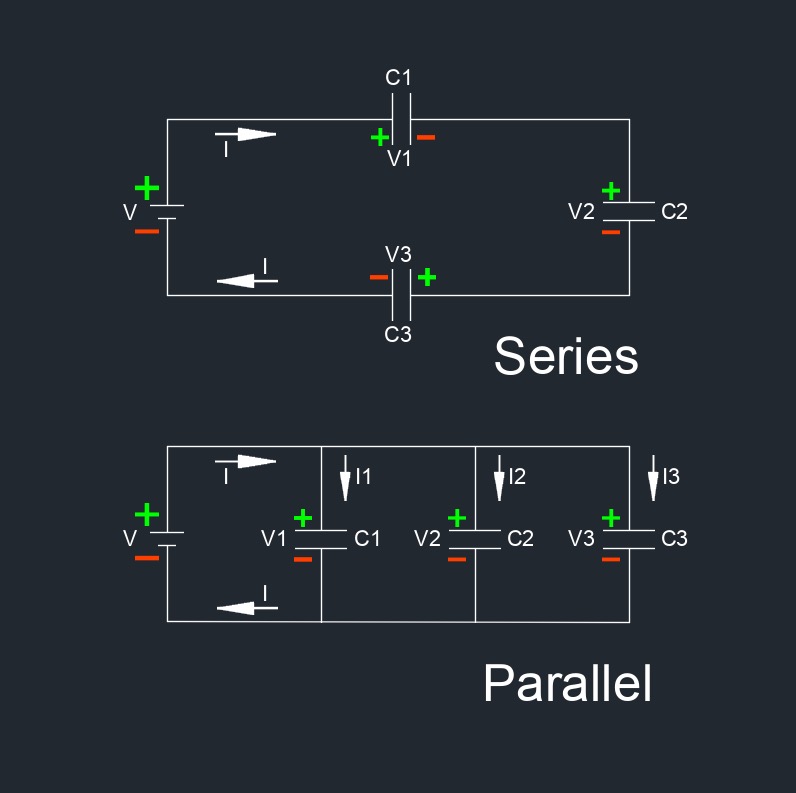
| \( \dfrac{1}{C_t} \;=\; \dfrac{1}{C_1} + \dfrac{1}{C_2} + \dfrac{1}{C_3} \; + ... +\; \dfrac{1}{C_n} \) (Series Circuit) | ||
| \(C_t \;=\; C_1 + C_2 + C_3 \; + ... + \; C_n \) (Parallel Citcuit) | ||
| Symbol | English | Metric |
| \(C\) = Capacitance | \(F\) | \(F\) |
| \( Q \) = Charge | \(C\) | \(C\) |
| \( V \) = Voltage | \(V\) | \(V\) |
Capacitor is a passive electronic component that stores electrical energy in an electric field. It consists of two conductive plates separated by a non-conductive insulating material called a dielectric. When voltage is applied across the plates, electric charge accumulates on them, creating an electric field between them. This stored charge creates a potential difference (voltage) across the capacitor.
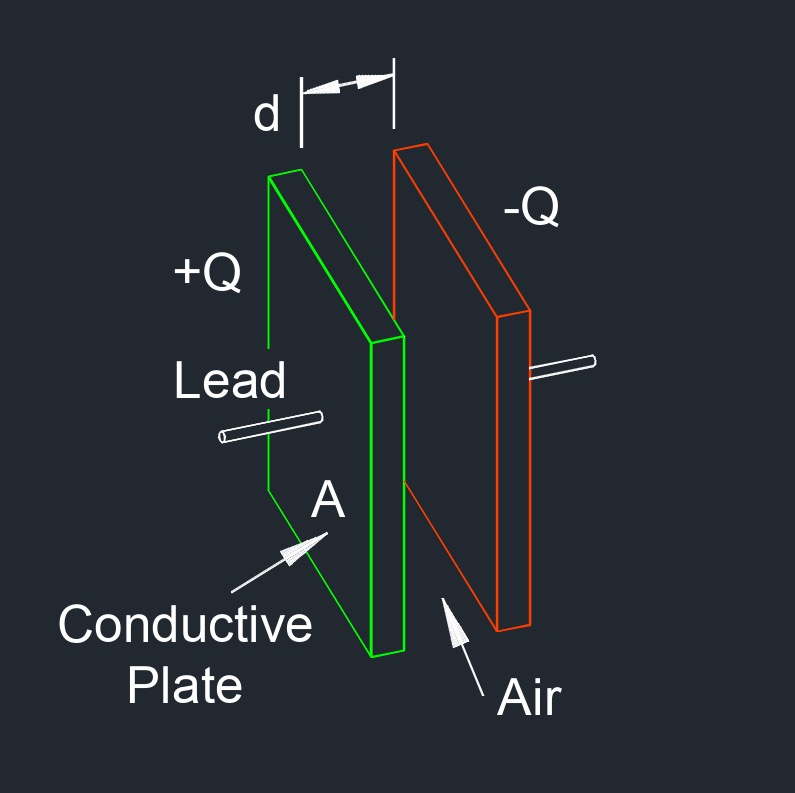
Capacitance of Parallel Plates with Air Between Formula |
||
| \(C \;=\; \epsilon_0 \cdot \dfrac{ A }{ d } \) | ||
| Symbol | English | Metric |
| \(C\) = Capacitance | \(F\) | \(F\) |
| \( \epsilon_0 \) (Greek symbol epsilon) = Permeability of Vacuum (Dielectric Constant) | \(in\;/\;sec\) | \(mm\;/\;s\) |
| \( A \) = Plate Area | \(in^2\) | \(mm^2\) |
| \( d \) = Distance Between Plates | \(in\) | \(mm\) |
 Capacitors are used in electronic circuits for various purposes, such as energy storage, power conditioning, filtering, signal coupling, and timing. They can store and release electrical energy rapidly, making them useful in applications where rapid changes in voltage are necessary. Capacitors come in various types and sizes, with different materials for the dielectric and construction, allowing them to have different characteristics such as capacitance, voltage rating, temperature stability, and frequency response. Capacitors with higher capacitance can store more charge for a given voltage, while those with lower capacitance store less charge. Capacitors also have a voltage rating, which specifies the maximum voltage they can withstand without breaking down the dielectric.
Capacitors are used in electronic circuits for various purposes, such as energy storage, power conditioning, filtering, signal coupling, and timing. They can store and release electrical energy rapidly, making them useful in applications where rapid changes in voltage are necessary. Capacitors come in various types and sizes, with different materials for the dielectric and construction, allowing them to have different characteristics such as capacitance, voltage rating, temperature stability, and frequency response. Capacitors with higher capacitance can store more charge for a given voltage, while those with lower capacitance store less charge. Capacitors also have a voltage rating, which specifies the maximum voltage they can withstand without breaking down the dielectric.
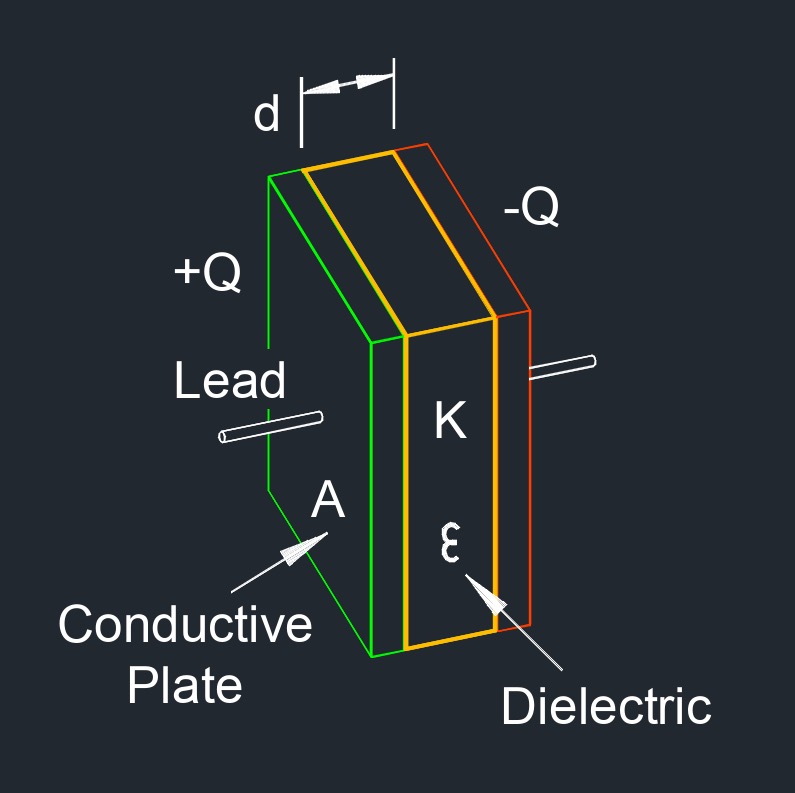
Capacitance of Parallel Plates with One Dielectric Between Formula |
||
| \(C \;=\; \kappa \cdot \epsilon_0 \cdot \dfrac{ A }{ d } \) | ||
| Symbol | English | Metric |
| \(C\) = Capacitance | \(F\) | \(F\) |
| \( \kappa \) (greek symbol kappa) = Dielectric Constant | \(dimensionless\) | \(dimensionless\) |
| \( \epsilon_0 \) (Greek symbol epsilon) = Permeability of Vacuum (Space) | \(in\;/\;sec\) | \(mm\;/\;s\) |
| \( A \) = Plate Area | \(in^2\) | \(mm^2\) |
| \( d \) = Distance Between Plates | \(in\) | \(mm\) |
How Capacitors Work
Charge Storage - When a voltage is applied across the two plates of a capacitor, electrons from one plate are attracted to the other plate, creating an electric field between them. Electrons accumulate on one plate, giving it a negative charge, while the other plate becomes positively charged due to the loss of electrons.
Dielectric - The dielectric material between the plates of the capacitor serves to increase the capacitance of the capacitor. Dielectric materials have high permittivity, which means they can store more electric charge per unit area of the plates compared to air or a vacuum.
Capacitance - The capacitance of a capacitor is a measure of its ability to store electrical charge and is determined by the size and separation of the plates as well as the properties of the dielectric material between them.
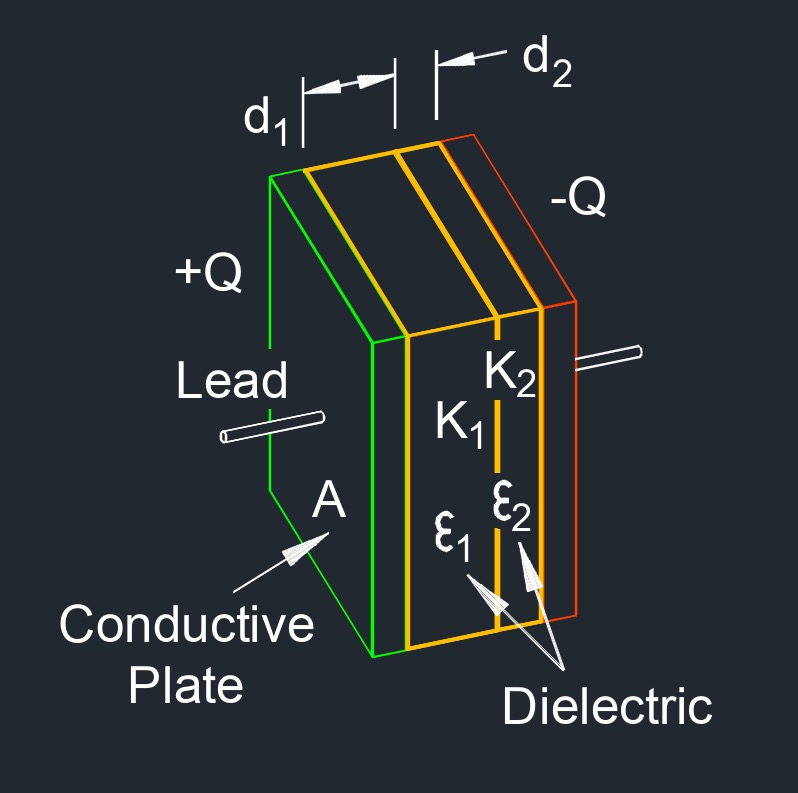
Capacitance of Parallel Plates with Two Dielectric Between Formula |
||
| \(C \;=\; \dfrac{ \epsilon_0 \cdot A }{ \dfrac{ d_1 }{ \kappa_1} + \dfrac{d_2 }{ \kappa_2} }\) | ||
| Symbol | English | Metric |
| \(C\) = Capacitance | \(F\) | \(F\) |
| \( \kappa_1, \kappa_2 \) (greek symbol kappa) = Dielectric Constant | \(dimensionless\) | \(dimensionless\) |
| \( \epsilon_0 \) (Greek symbol epsilon) = Permeability of Vacuum (Space) | \(in\;/\;sec\) | \(mm\;/\;s\) |
| \( A \) = Plate Area | \(in^2\) | \(mm^2\) |
| \( d_1, d_2 \) = Distance Between Plates | \(in\) | \(mm\) |
 Charging and Discharging - When a capacitor is connected to a voltage source, it charges up until the voltage across its plates equals the applied voltage. The time it takes for a capacitor to charge or discharge depends on its capacitance and the resistance of the circuit it is connected to.
Charging and Discharging - When a capacitor is connected to a voltage source, it charges up until the voltage across its plates equals the applied voltage. The time it takes for a capacitor to charge or discharge depends on its capacitance and the resistance of the circuit it is connected to.
Energy Storage - Capacitors store energy in the form of an electric field between their plates. The amount of energy stored in a capacitor is proportional to the square of the voltage across its plates and its capacitance.
Transient Response - Capacitors react to changes in voltage by either sourcing or sinking current to maintain a constant voltage across their plates. This property makes capacitors useful in filtering, smoothing, and stabilizing electrical signals in circuits.
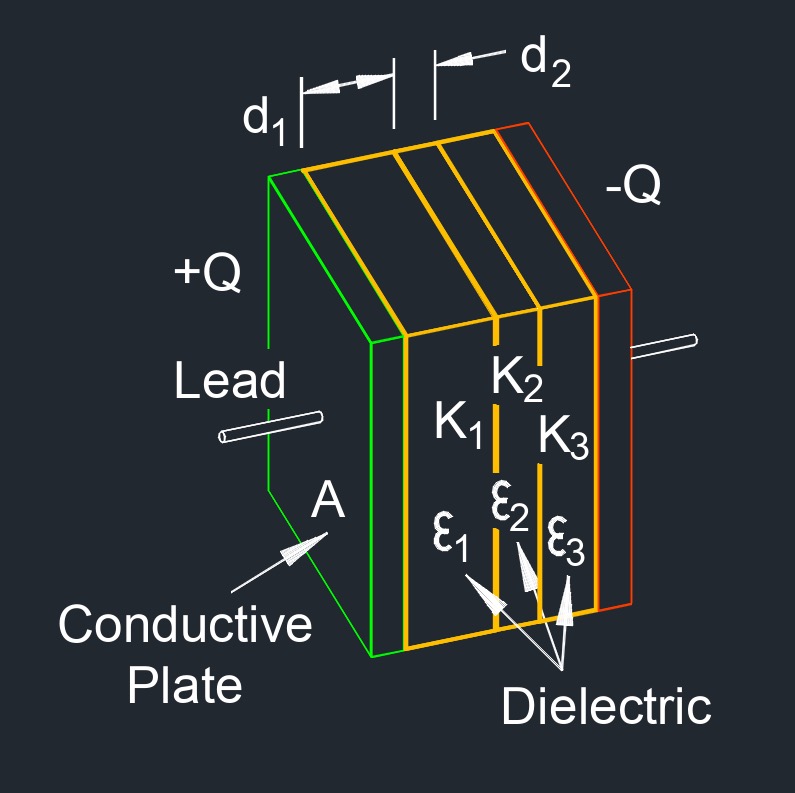
Capacitance of Parallel Plates with Three Dielectric Between Formula |
||
| \(C \;=\; \dfrac{ \epsilon_0 \cdot A }{ \dfrac{d_1 }{ \kappa_1} + \dfrac{d_2 }{ \kappa_2} + \dfrac{d_3 }{ \kappa_3} }\) | ||
| Symbol | English | Metric |
| \(C\) = Capacitance | \(F\) | \(F\) |
| \( \kappa_1, \kappa_2, \kappa_3 \) (greek symbol kappa) = Dielectric Constant | \(dimensionless\) | \(dimensionless\) |
| \( \epsilon_0 \) (Greek symbol epsilon) = Permeability of Vacuum (Space) | \(in\;/\;sec\) | \(mm\;/\;s\) |
| \( A \) = Plate Area | \(in^2\) | \(mm^2\) |
| \( d_1, d_2, d_3 \) = Distance Between Plates | \(in\) | \(mm\) |
Types of Capacitors - There are various types of capacitors, including ceramic capacitors, electrolytic capacitors, tantalum capacitors, and film capacitors. Each type has different characteristics such as capacitance range, voltage rating, temperature stability, and frequency response, making them suitable for different applications.
Applications - Capacitors are used in a wide range of electronic and electrical circuits for various purposes, including energy storage, power factor correction, noise filtering, timing circuits, decoupling, and coupling. They are essential components in devices such as power supplies, amplifiers, filters, and oscillators.
How Capacitors Work
Charge Storage - When a voltage is applied across the two plates of a capacitor, electrons from one plate are attracted to the other plate, creating an electric field between them. Electrons accumulate on one plate, giving it a negative charge, while the other plate becomes positively charged due to the loss of electrons.
Dielectric - The dielectric material between the plates of the capacitor serves to increase the capacitance of the capacitor. Dielectric materials have high permittivity, which means they can store more electric charge per unit area of the plates compared to air or a vacuum.
Capacitance - The capacitance of a capacitor is a measure of its ability to store electrical charge and is determined by the size and separation of the plates as well as the properties of the dielectric material between them.
Charging and Discharging - When a capacitor is connected to a voltage source, it charges up until the voltage across its plates equals the applied voltage. The time it takes for a capacitor to charge or discharge depends on its capacitance and the resistance of the circuit it is connected to.
Energy Storage - Capacitors store energy in the form of an electric field between their plates. The amount of energy stored in a capacitor is proportional to the square of the voltage across its plates and its capacitance.
Transient Response - Capacitors react to changes in voltage by either sourcing or sinking current to maintain a constant voltage across their plates. This property makes capacitors useful in filtering, smoothing, and stabilizing electrical signals in circuits.
Types of Capacitors - There are various types of capacitors, including ceramic capacitors, electrolytic capacitors, tantalum capacitors, and film capacitors. Each type has different characteristics such as capacitance range, voltage rating, temperature stability, and frequency response, making them suitable for different applications.
Applications - Capacitors are used in a wide range of electronic and electrical circuits for various purposes, including energy storage, power factor correction, noise filtering, timing circuits, decoupling, and coupling. They are essential components in devices such as power supplies, amplifiers, filters, and oscillators.
Capacitor Types
Capacitors come in various types, each with specific characteristics suited for different applications. These are some of the most common types of capacitors, each with unique characteristics suited for specific applications in electronics and electrical engineering.
Ceramic Capacitor - These capacitors use a ceramic material as the dielectric, sandwiched between two metal plates. They are widely used due to their small size, low cost, and high reliability.
- Multilayer Ceramic Capacitor - Consist of multiple layers of ceramic and metal electrodes stacked together, offering high capacitance values in a small footprint.
- Disc Ceramic Capacitor - Disc-shaped capacitors with ceramic dielectric, commonly used in high voltage applications.
Electrolytic Capacitor - Electrolytic capacitors use an electrolyte solution as one of the capacitor plates. They offer relatively high capacitance values and are polarized, meaning they have a specific orientation for proper operation.
- Aluminum Electrolytic Capacitor - Have aluminum foil as one of the electrodes and use an electrolyte solution. They are commonly used in power supply circuits.
- Tantalum Electrolytic Capacitor - Use a tantalum-based electrolyte and are known for their high capacitance density and stability. They are used in applications requiring smaller size and higher reliability compared to aluminum electrolytic capacitors.
Film Capacitor - Film capacitors use a thin plastic film as the dielectric, with metal electrodes deposited on the film. They offer good stability, low leakage, and low dielectric absorption.
- Polyester Film Capacitor (Mylar) - Made with polyester film as the dielectric and suitable for general purpose applications.
- Polypropylene Film Capacitor - Use polypropylene film as the dielectric, offering better temperature stability and lower dielectric losses compared to polyester film capacitors. They are often used in audio and precision applications.
- Polyethylene Film Capacitor - Use polyethylene film as the dielectric and are known for their high insulation resistance and stability at high temperatures.
- Metalized Film Capacitor - Metalized film capacitors have a metalized layer directly on the dielectric film, eliminating the need for separate metal electrodes. They offer self-healing properties and are often used in high-frequency applications.

