- Home
- Science
- Mathematics
- Physics
- Engineering
- Datasheets
- Accessory Datasheets
- Fastener Datasheets
- Fitting Datasheets
- Flange Datasheets
- Blind Flange Datasheets
- Ductile Iron Flange Datasheets
- Expander Flange Datasheets
- Flange Bolt Datasheets
- Lap Joint Flange Datasheets
- Orifice Flange Datasheets
- Slip-On Flange Datasheets
- Socket Flange Datasheets
- Standard Connection Flange Datasheets
- Studding Outlet Flange Datasheets
- Threaded Flange Datasheets
- Weld Neck Flange Datasheets
- Gasket Datasheets
- Pipe & Tubing Dimensions
- Piping Layout Information
- Valve Datasheets
- Standards
- Store
- The World

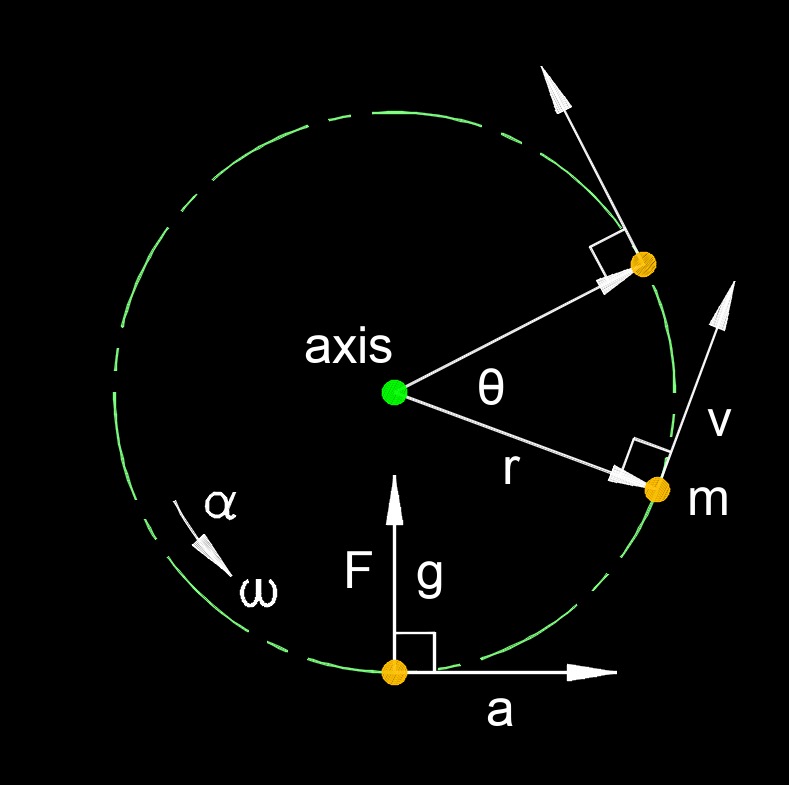 When an object makes changes in its angular velocity at different times that is an average angular velocity of any given velocities.
When an object makes changes in its angular velocity at different times that is an average angular velocity of any given velocities. 