Centrifugal Acceleration
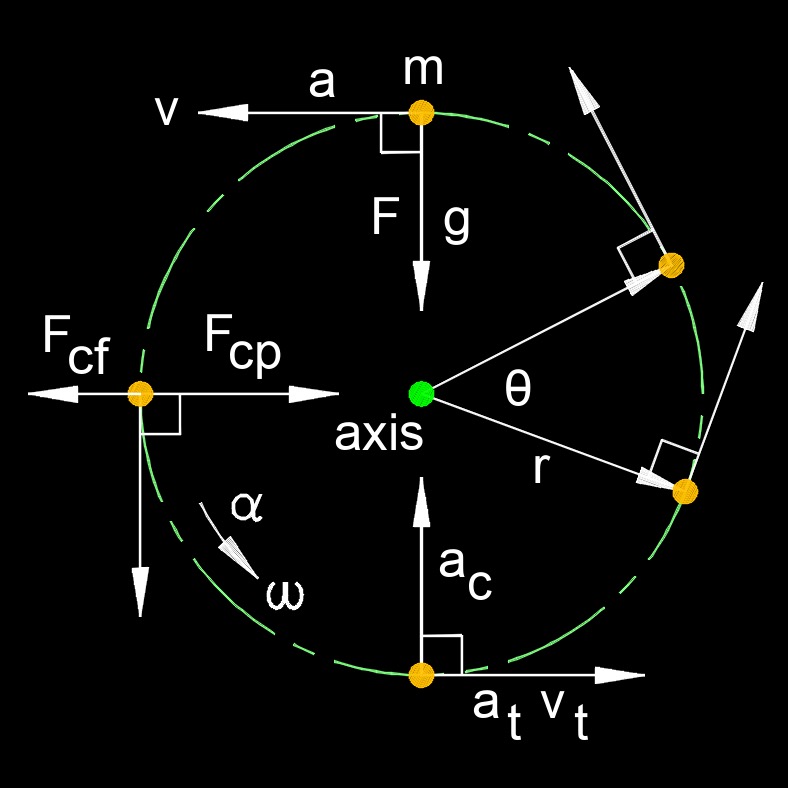Centrifugal acceleration, abbreviated as \(a_c\), also called centrifugal force or radial acceleration, is the apparent force that acts on an object moving in a circular path. It is not a real force in the sense of being caused by an interaction between objects but rather an apparent force that arises due to the object's inertia. Centrifugal acceleration is a result of the object's tendency to move in a straight line, according to Newton's first law of motion, combined with its constrained circular motion. When an object moves in a circular path, it constantly changes direction, which means it is accelerating. Centrifugal acceleration points outward from the center of the circular path and is always directed away from the center. This means that the faster an object moves or the smaller the radius of its circular path, the greater the centrifugal acceleration it experiences.
It's important to note that centrifugal acceleration is not a true force like gravity or electromagnetism but rather a result of an object's inertia and its motion in a curved path. It is often used in engineering and physics to analyze and design systems involving rotating objects, such as centrifuges, amusement park rides, and vehicles taking turns on curved roads.
Centrifugal Acceleration formula |
||
|
\( a_c = v_t^2 \;/\; r \) (Centrifugal Acceleration) \( v_t = \sqrt{ a_c \; r } \) \( r = v_t^2 \;/\; a_c \) |
||
| Symbol | English | Metric |
| \( a_c \) = centrifugal acceleration | \(ft / sec^2\) | \(m / s^2\) |
| \( v_t \) = tangential velocity | \(ft / sec\) | \(m / s\) |
| \( r \) = radius | \(ft\) | \(m\) |
Tags: Acceleration