Total Work
Total Work formula |
||
|
\( W_t \;=\; \dfrac{1}{2}\cdot m \cdot v_f^2 - \dfrac{1}{2}\cdot m \cdot v_i^2 \) (Total Work) \( m \;=\; \dfrac{ 2 \cdot W }{ v_f^2 - v_i^2 } \) \( v_f \;=\; \sqrt{ \dfrac{ 2 \cdot ( W + \dfrac{1}{2}\cdot m \cdot v_i^2 ) }{ m } }\) \( v_i \;=\; \sqrt{ v_f^2 - \dfrac{ 2 \cdot W }{ m } }\) |
||
| Symbol | English | Metric |
| \( W_t \) = work | \(ft^3\;/\;sec\) | \(m^3\;/\;s\) |
| \( m \) = mass | \(lbm\) | \(kg\) |
| \( v_f \) = final velocity | \(ft\;/\;sec\) | \(m\;/\;s\) |
| \( v_i \) = initial velocity | \(ft\;/\;sec\) | \(m\;/\;s\) |
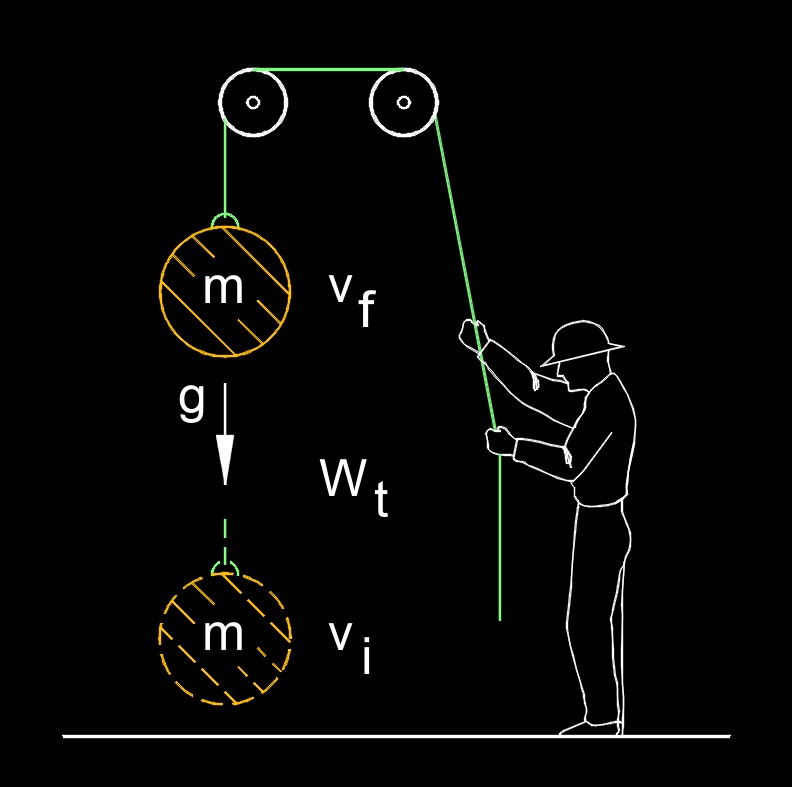 Total work, abbreviated as \(W_t\), is the cumulative effect of work done on an object or by an object in a given situation. Work is a concept in physics that represents the transfer of energy through the application of a force over a certain distance. When multiple forces act on an object or when an object is subjected to multiple displacements, the total work takes into account the net effect of all these individual works.
Total work, abbreviated as \(W_t\), is the cumulative effect of work done on an object or by an object in a given situation. Work is a concept in physics that represents the transfer of energy through the application of a force over a certain distance. When multiple forces act on an object or when an object is subjected to multiple displacements, the total work takes into account the net effect of all these individual works.
If the work done by a force is positive, it implies that the force is doing work on the object (adding energy to it). If the work done by a force is negative, it means that the force is taking energy away from the object (removing energy from it). The net total work gives a clear picture of the overall effect of all the forces involved.
It's important to note that if work is done on an object, its energy can change. The work-energy theorem states that the net work done on an object is equal to the change in its kinetic energy. In situations where an object undergoes a displacement while multiple forces act on it, calculating the total work requires considering both the magnitudes and directions of the individual works. The sign of each work term (positive or negative) indicates whether the force is aiding or opposing the displacement.
Total work is a fundamental concept in understanding how energy is transferred and transformed in various physical systems. It's used to analyze mechanical systems, calculate energy changes, and predict the outcomes of various interactions.

