Gauss's Law for Electricity Formula |
||
| \( \triangledown \cdot E \;=\; \dfrac{ \rho }{ \varepsilon_0 } \) | ||
| Symbol | English | Metric |
| \( \triangledown \) = Represents Divergence (How Much a Field Spreads Out) | \(dimensionless\) | \(dimensionless\) |
| \( E \) = Electric Field Vector | \(N\;/\;C\) | \(V\;/\;m\) |
| \( \rho \) = Electric Charge Density | \(in^2\) | \(mm^2\) |
| \( \varepsilon_0 \) = Permittivity Free Space (\(8.85 \;x\; 10^{-12}\;F\;/\;m\) ) | - | \(H\;/\;m\) |
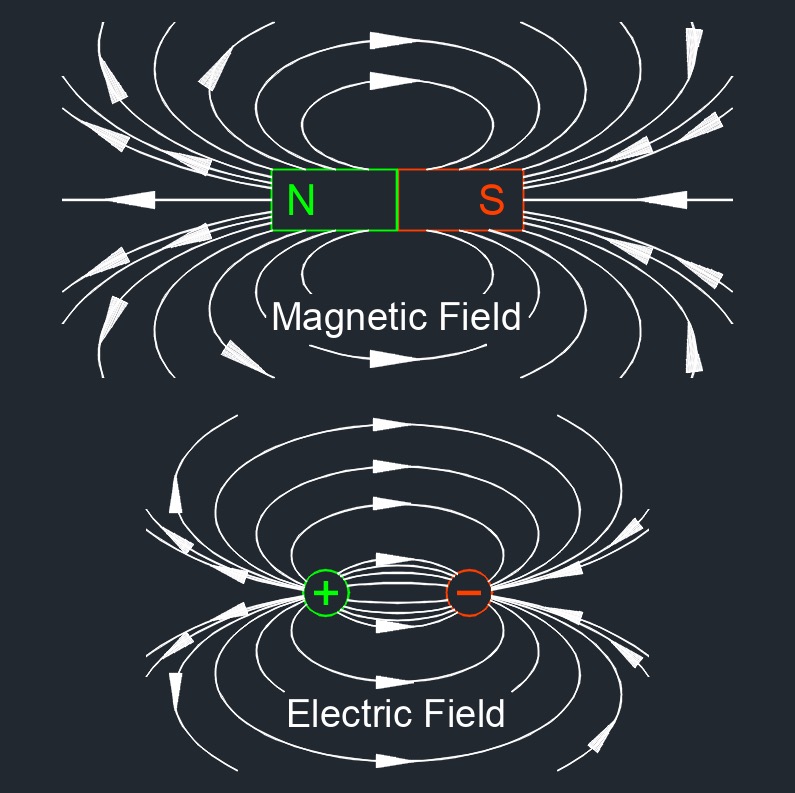Gauss’s law for electricity is a principle in electromagnetism that relates the distribution of electric charge to the resulting electric field. It states that the total electric flux passing through a closed surface, often referred to as a Gaussian surface, is directly proportional to the net electric charge enclosed within that surface. Mathematically, this is expressed as the surface integral of the electric field over the closed surface being equal to the enclosed charge divided by the permittivity of free space. In simpler terms, Gauss’s Law shows how charges act as sources or sinks of electric field lines, with positive charges radiating field lines outward and negative charges pulling them inward. This law is especially powerful in solving problems with high symmetry, such as spherical, cylindrical, or planar charge distributions, because it simplifies the calculation of electric fields in those cases.
