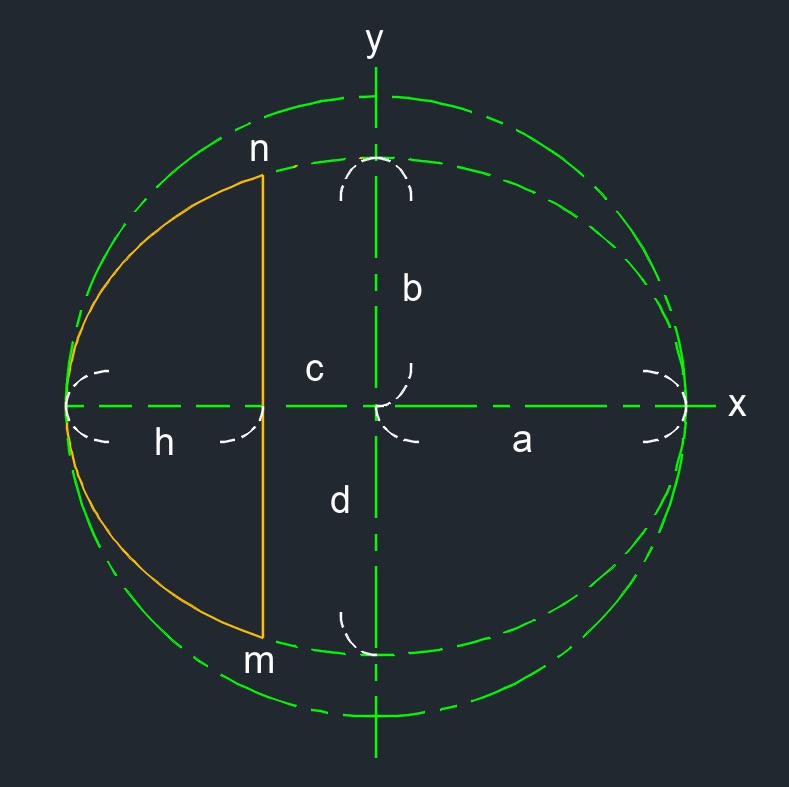
Segment of an ellipse is the region enclosed by a chord of an ellipse and the arc of the ellipse connecting the two endpoints of that chord. A chord is a straight line segment whose endpoints both lie on the ellipse, while the arc is the curved portion of the ellipse between those same endpoints. The segment is therefore a two-dimensional area bounded by one straight edge (the chord) and one curved edge (the elliptical arc).
Segment Area formula |
||
| \(\large{ A_{area} \;=\; \dfrac{c\cdot d}{4} \; \left[ arccos \left( 1-\dfrac{2\cdot h}{c} \right) - \left( 1-\dfrac{2\cdot h}{c} \right) \cdot \sqrt{ \dfrac{4\cdot h}{c} } - \dfrac{4\cdot h^2}{c^2} \right] }\) | ||
| Symbol | English | Metric |
| \( A_{area} \) = area | \( in^2 \) | \( mm^2 \) |
| \( h \) = height | \( in \) | \( mm \) |
| \( c \) = major axis | \( in \) | \( mm \) |
| \( d \) = minor axis | \( in \) | \( mm \) |
- Ellipse segment (a two-dimensional figure) is an interior part of an ellipse bound by a chord and an ellipse.
- Chord is a line segment on the interior of the ellipse.
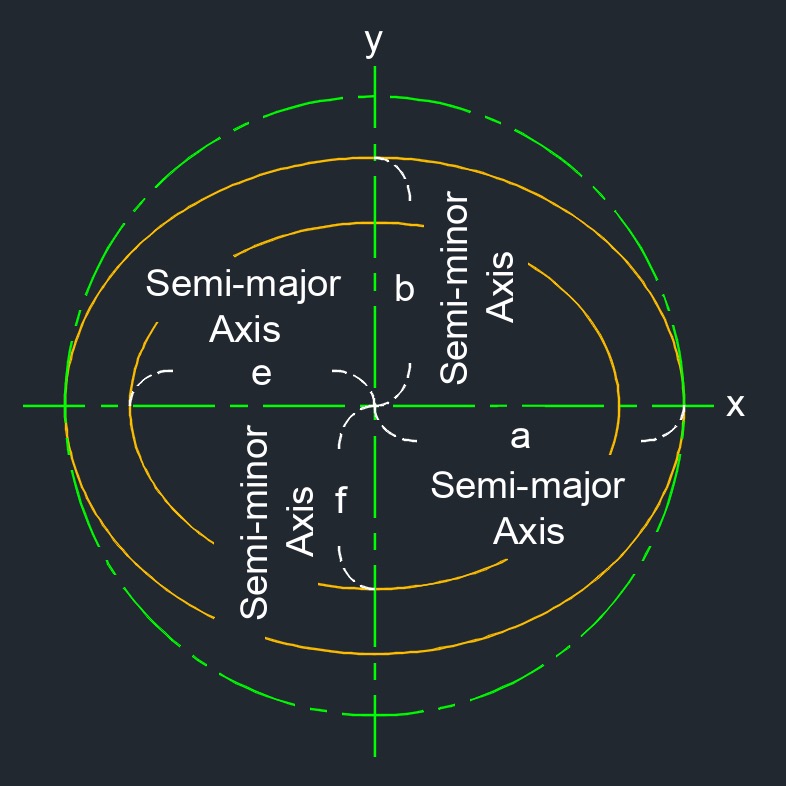
- Major axis is always the longest axis in an ellipse.
Minor axis is always the shortest axis in an ellipse.- Semi-major axis is half of the longest axis of an ellipse.
- Semi-minor axis is half of the shortest axis of an ellipse.
