Ideal Gas Law Volume Formula |
||
|
\( V \;=\; \dfrac{ n \cdot R \cdot T }{ p }\) (Ideal Gas Law Volume) \( n \;=\; \dfrac{ p \cdot V }{ R \cdot T }\) \( R \;=\; \dfrac{ p \cdot V }{ n \cdot T }\) \( T \;=\; \dfrac{ p \cdot V }{ n \cdot R }\) \( p \;=\; \dfrac{ n \cdot R \cdot T }{ V }\) |
||
| Symbol | English | Metric |
| \( V \) = Gas Volume | \( in^3 \) | \( mm^3 \) |
| \( n \) = Number of Moles of Gas | \(dimensionless\) | \(dimensionless\) |
| \( R \) = Specific Gas Constant (Gas Constant) | \(ft-lbf\;/\;lbm-R\) | \(J\;/\;kg-K\) |
| \( T \) = Gas Temperature | \( R \) | \( K \) |
| \( p \) = Gas Pressure | \(lbf\;/\;in^2\) | \(Pa\) |
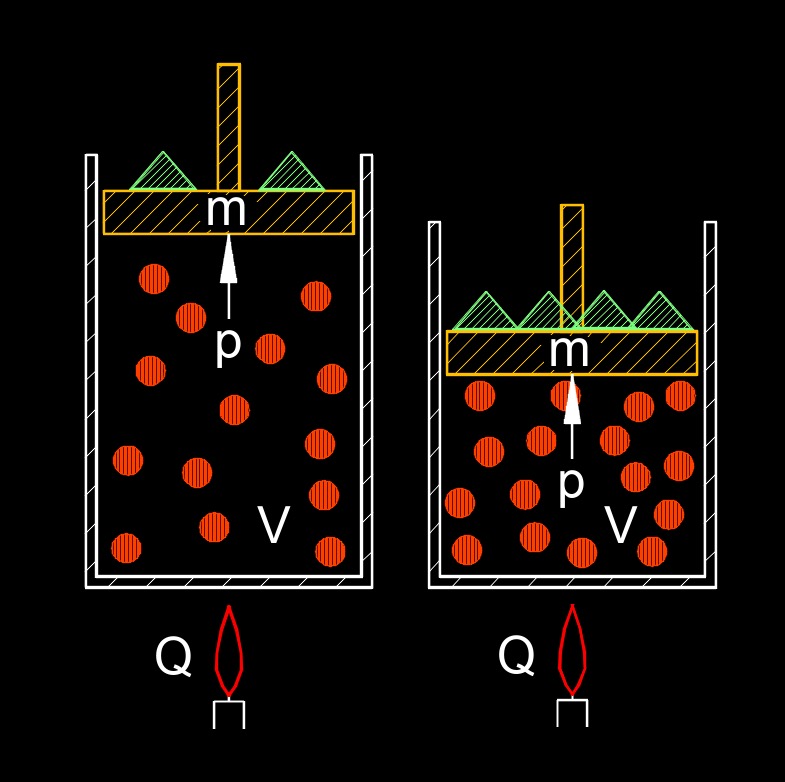The ideal gas law, PV=nRT, can be rearranged to solve for the volume of a gas. This relationship indicates that the volume occupied by an ideal gas is directly proportional to the number of moles of the gas and its absolute temperature, while it is inversely proportional to the pressure exerted on it. The universal gas constant acts as the proportionality factor. Consequently, at a constant temperature and pressure, a larger amount of gas (more moles) will occupy a greater volume. Similarly, if the amount of gas and pressure are kept constant, increasing the temperature will cause the volume to expand. Conversely, increasing the pressure on a fixed amount of gas at a constant temperature will result in a decrease in volume.
