- See Article - Beam Design Formulas
beam fixed at both ends - Uniformly Distributed Load formulas |
||
|
\( R \;=\; V \;=\; \dfrac{ w \cdot L }{ 2 }\) \( V_x \;=\; w \cdot \left( \dfrac{ L }{ 2 } - x \right) \) \( M_{max} \; (at \;ends ) \;=\; \dfrac{ w\cdot L^2 }{ 12 } \) \( M_1 \; (at\; center ) \;=\; \dfrac{ w \cdot L^2 }{ 24 } \) \( M_x \;=\; \dfrac{w}{12} \cdot ( 6 \cdot L \cdot x - L^2 - 6 \cdot x^2 ) \) \( M_{max} \; (at \;center ) \;=\; \dfrac{ w \cdot L^4 }{ 384 \cdot \lambda \cdot I } \) \( \Delta_x \;=\; \dfrac{ w \cdot x^2 }{ 24 \cdot \lambda \cdot I } \cdot ( L - x ) ^2 \) \( x \; (points \;of \;contraflexure ) \;=\; (\sqrt{3} - 3 ) \cdot L \) |
||
| Symbol | English | Metric |
| \( R \) = Reaction Load at Bearing Point | \(lbf\) | \(N\) |
| \( V \) = Maximum Shear Force | \(lbf\) | \(N\) |
| \( M \) = Maximum Bending Moment | \(lbf - in\) | \(N - mm\) |
| \( \Delta \) = Deflection or Deformation | \(in\) | \(mm\) |
| \( x \) = Horizontal Distance from Reaction to Point on Beam | \(in\) | \(mm\) |
| \( w \) = Load per Unit Length | \(lbf\;/\;in\) | \(N\;/\;m\) |
| \( L \) = Span Length of the Bending Member | \(in\) | \(mm\) |
| \( \lambda \) (Greek symbol lambda) = Modulus of Elasticity | \(lbf\;/\;in^2\) | \(Pa\) |
| \( I \) = Second Moment of Area (Moment of Inertia) | \(in^4\) | \(mm^4\) |
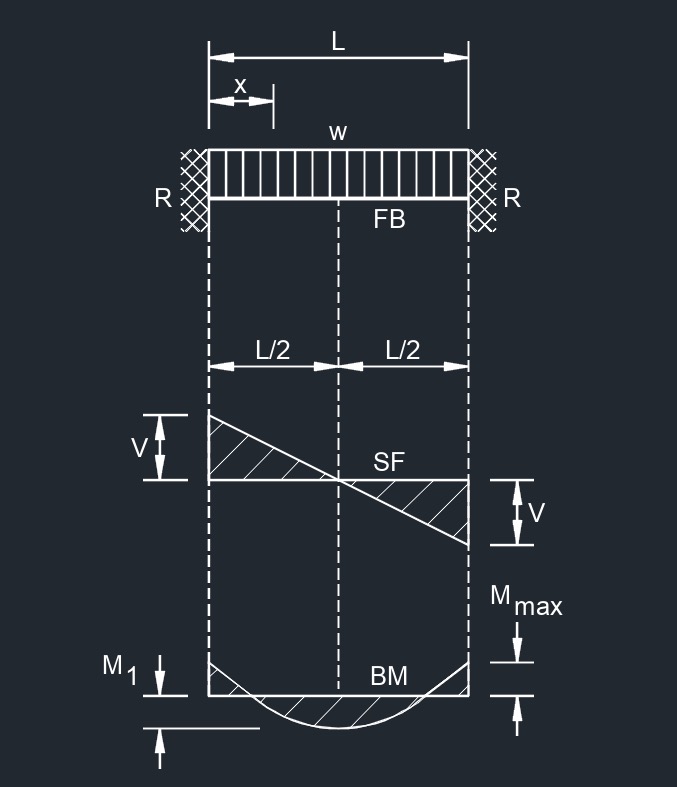
Diagram Symbols
Bending moment diagram (BMD) - Used to determine the bending moment at a given point of a structural element. The diagram can help determine the type, size, and material of a member in a structure so that a given set of loads can be supported without structural failure.
Free body diagram (FBD) - Used to visualize the applied forces, moments, and resulting reactions on a structure in a given condition.
Shear force diagram (SFD) - Used to determine the shear force at a given point of a structural element. The diagram can help determine the type, size, and material of a member in a structure so that a given set of loads can be supported without structural failure.
Uniformly distributed load (UDL) - A load that is distributed evenly across the entire length of the support area.
