Area of 3 Overlapping Circles formulas |
||
|
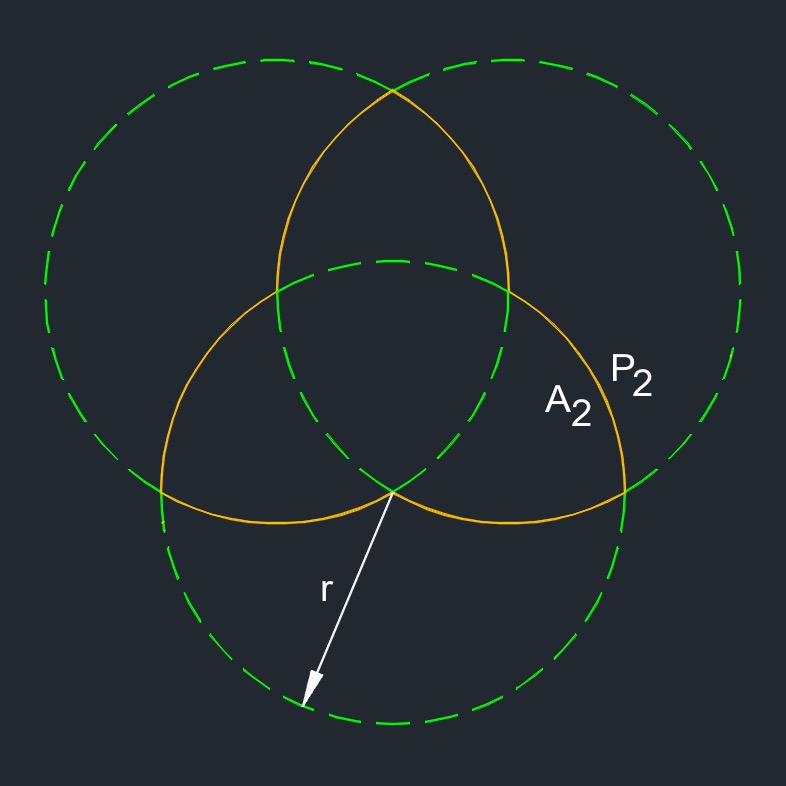
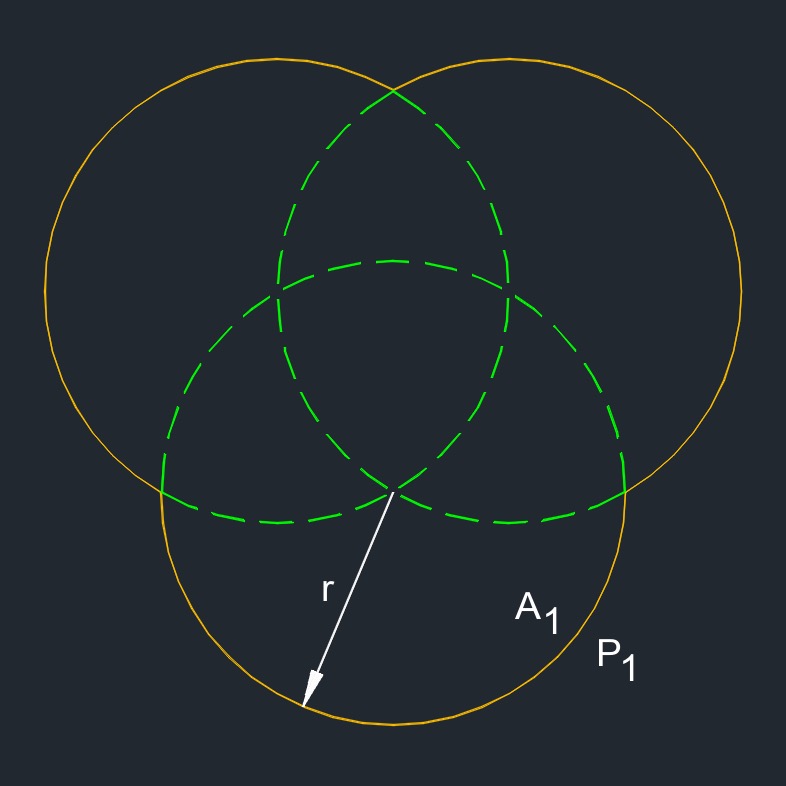
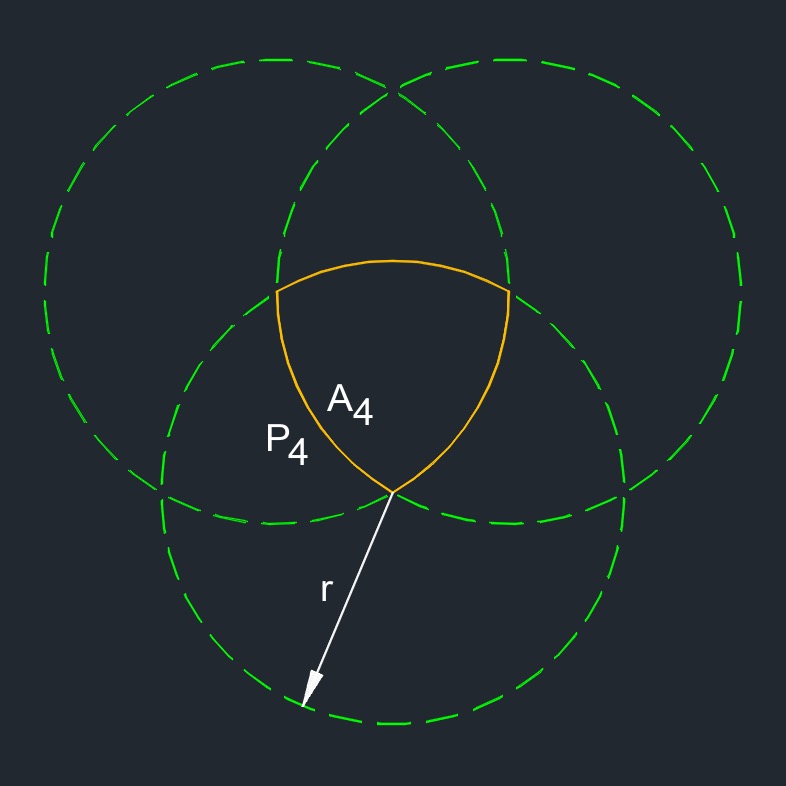
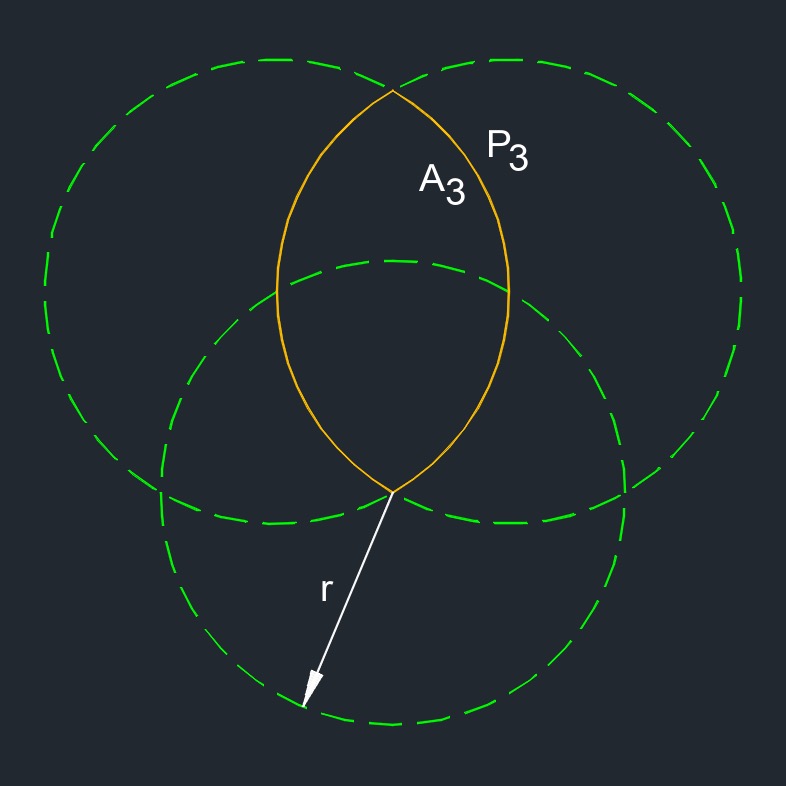
\( A_1 \;=\; ( 3 \cdot \pi \cdot r^2 ) - ( 3 \cdot A_3 ) + A_4 \) \( A_2 \;=\; ( 3 \cdot A_3 ) - (2 \cdot A_4 ) \) \( A_3 \;=\; \left[ \; \left(\;2 \cdot \dfrac{\pi }{ 3 } \; \right) - \sqrt{ \dfrac{ 3 }{ 4 } }\;\; \right] \cdot r^2 \) \( A_4 \;=\; ( \pi - \sqrt{3}\;) \cdot \dfrac{ r^2 }{ 2 } \) |
||
| Symbol | English | Metric |
| \( A \) = area | \(ft^2\) | \(m^2\) |
| \( \pi \) = Pi | \(3.141 592 653 ...\) | \(3.141 592 653 ...\) |
| \( r \) = radius | \(ft\) | \(m\) |
- 3 overlapping circles (a two-dimensional figure) with equal length arcs connecting at the vertices.
Perimeter of 3 Overlapping Circles formulas |
||
|
\( P_1 \;=\; 3 \cdot \pi \cdot r \) \( P_2 \;=\; 2 \cdot \pi \cdot r \) \( P_3 \;=\; \dfrac{ 4 }{ 3 } \cdot \pi \cdot r \) \( P_4 \;=\; \pi \cdot r \) |
||
| Symbol | English | Metric |
| \( P \) = perimeter | \(ft\) | \(m\) |
| \( \pi \) = Pi | \(3.141 592 653 ...\) | \(3.141 592 653 ...\) |
| \( r \) = radius | \(ft\) | \(m\) |
