Tangential acceleration formula |
||
|
\( a_t \;=\; r \cdot \alpha \) (Tangential Acceleration) \( r \;=\; \dfrac{ a_t }{ \alpha }\) \( \alpha \;=\; \dfrac{ a_t }{ r }\) |
||
| Symbol | English | Metric |
| \( a_t \) = tangential acceleration | \(ft / sec^2\) | \(m / s^2\) |
| \( r \) = radius of object rotation | \( ft \) | \( m \) |
| \( \alpha \) (Greek symbol alpha) = angular acceleration | \(deg / sec^2\) | \(rad / s^2\) |
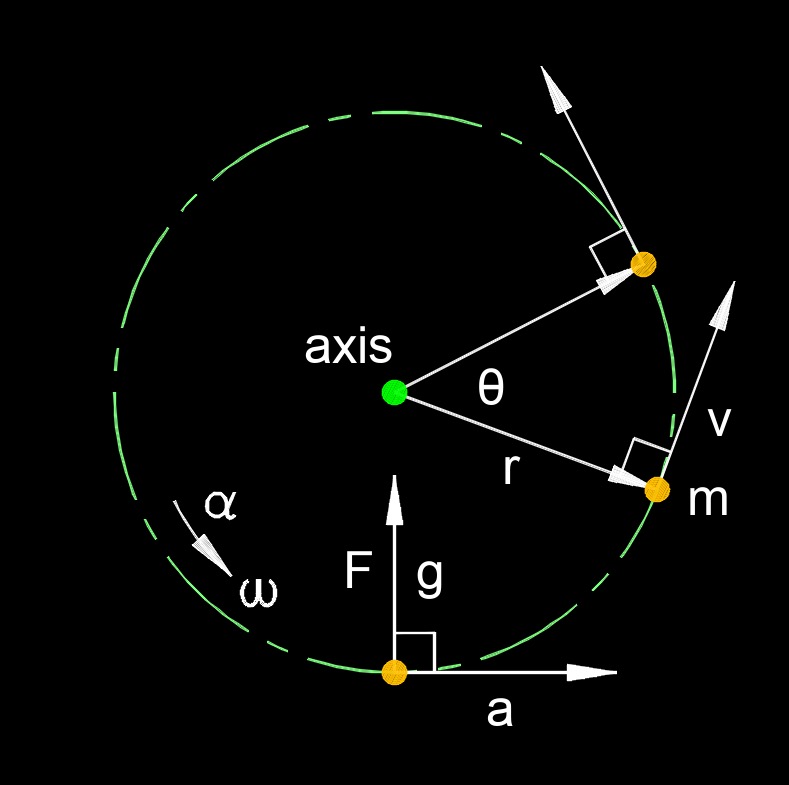Tangential acceleration, abbreviated as \(a_t\), is a term used in physics to describe the rate of change of an object's tangential velocity with respect to time. It is one component of the total acceleration experienced by an object in curved or circular motion. Tangential acceleration specifically refers to how an object's speed changes as it moves along a curved path.
Tangential acceleration can be positive or negative, depending on whether an object is speeding up or slowing down as it moves along a curved path. For example, when an object is in uniform circular motion, its tangential acceleration is zero because its speed remains constant. However, if the object is speeding up or slowing down while moving in a circle, it experiences a non-zero tangential acceleration.
Tangential acceleration formula |
||
|
\( a_t \;=\; \dfrac{ \Delta \omega }{ \Delta t }\) (Tangential Acceleration) \( \Delta \omega \;=\; a_t \cdot \Delta t \) \( \Delta t \;=\; \dfrac{ \Delta \omega }{ a_ t }\) |
||
| Symbol | English | Metric |
| \( a_t \) = tangential acceleration | \(ft / sec^2\) | \(m / s^2\) |
| \( \Delta \omega \) (Greek symbol omega) = angular velocity differential | \(deg / sec\) | \(rad / s\) |
| \( \Delta t \) = time differential | \(sec \) | \( s \) |
In many cases of circular or curved motion, the tangential acceleration works in conjunction with centripetal acceleration, which is the acceleration directed toward the center of the circular path and is responsible for keeping the object in its curved trajectory. Together, these two components of acceleration describe the overall motion of an object in a circular path.
