Rotational Motion Formula |
||
|
\( \theta \;=\; \omega \cdot t \) (Rotational Motion) \( \omega \;=\; \dfrac{ \theta }{ t }\) \( t \;=\; \dfrac{ \theta }{ \omega }\) |
||
| Symbol | English | Metric |
| \( \theta \) (Greek symbol theta) = Angular Position (Rotational Motion) | \(deg\) | \(rad\) |
| \( \omega \) (Greek symbol omega) = Average Angular Velocity | \(deg\;/\;sec\) | \(rad\;/\;s\) |
| \( t \) = Time | \(sec\) | \(s\) |
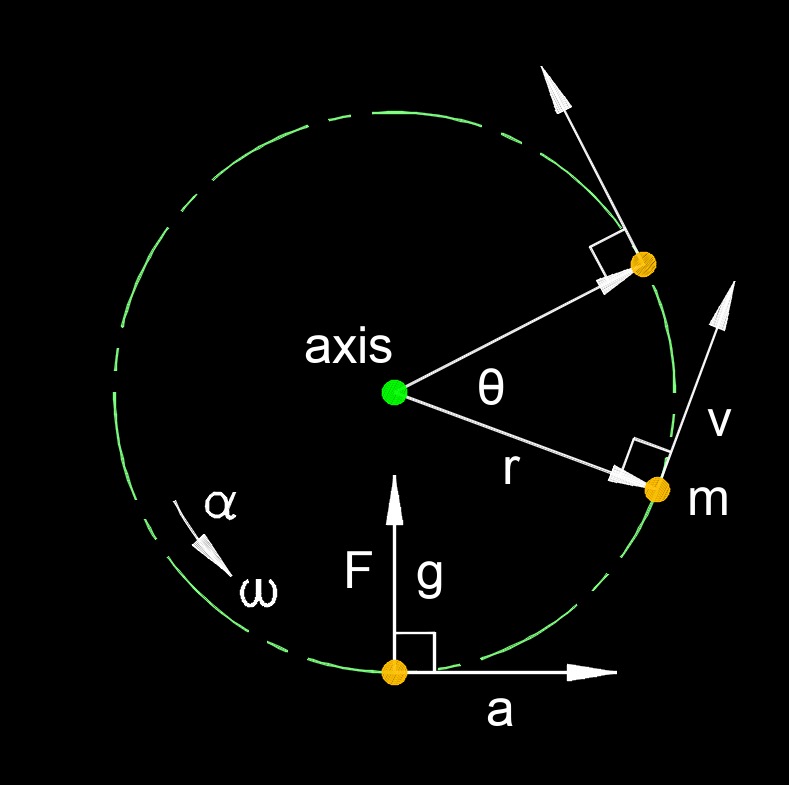Rotational motion, abbreviared as \( \theta\) (Greek symbol theta), also called rotational dynamics or circular motion, refers to the motion of an object around a fixed axis or center of rotation. Unlike linear motion, which involves movement along a straight line, rotational motion occurs when an object rotates or spins around a central point. Key concepts in rotational motion include angular displacement, angular velocity, and angular acceleration. These quantities are analogous to their linear counterparts in linear motion.
Rotational motion has numerous applications in various fields, such as physics, engineering, and everyday life. Examples include the spinning of wheels, rotation of celestial bodies, the movement of gears, gyroscopic stability, and the behavior of spinning tops or other rotating objects. Understanding rotational motion is essential for analyzing the dynamics of rotating machinery, designing systems involving rotating components, and explaining phenomena related to spinning objects.
