Work-Energy Theorem

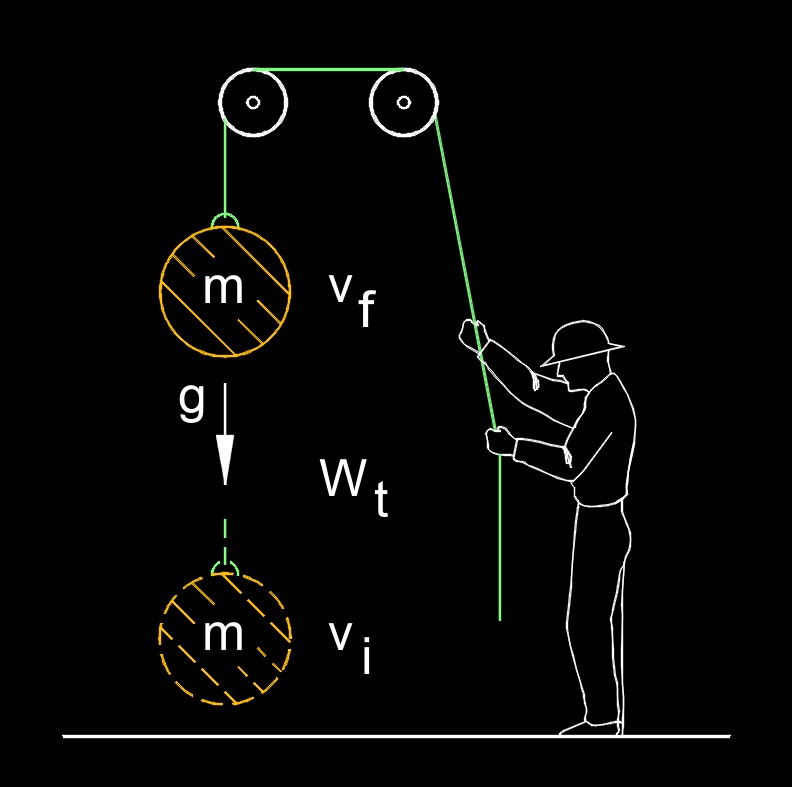Work-energy theorem, abbreviated as \(W\), also called work-energy principle, is the change in the kinetic energy of an object is equal to the net work done on the object.  Energy is the capacity of doing work.  Energy is never created or destroyed but external work performed on a conservative system goes into changing the system's total energy.

The work-energy theorem helps describe the relationship between the forces acting on an object and the resulting motion.  If work is done on an object, it will experience a change in kinetic energy. This theorem is a useful tool in analyzing and solving problems related to the motion of objects under the influence of forces.

It's important to note that work can be done by various forces, such as gravitational forces, applied forces, and frictional forces.  The work-energy theorem provides a way to quantify the energy changes associated with the work done on an object.

 

Work-Energy theorem formula
\( W_{net} = \Delta KE \)
Symbol	English	Metric
\( W \) = Work	\(ft^3\;/\;sec\)	\(m^3\;/\;s\)
\( \Delta KE \) = Kinetic Energy Change	\(lbf - ft\)	\(J\)

 

Work-Energy theorem formula
\( W =  KE_f - KE_i \)     (Work-Energy Theorem) \( KE_f =  W + KE_i \) \( KE_i =  KE_f - W \)
Symbol	English	Metric
\(\large{ W }\) = Work	\(ft^3\;/\;sec\)	\(m^3\;/\;s\)
\(\large{ KE_f }\) = Final Kinetic Energy	\(lbf - ft\)	\(J\)
\(\large{ KE_i }\) = Initial Kinetic Energy	\(lbf - ft\)	\(J\)