Tension Formula |
||
|
\( T \;=\; W + m \cdot a \) (Tension) \( W \;=\; T - m \cdot a \) \( m \;=\; \dfrac{ T - W }{ a }\) \( a \;=\; \dfrac{ T - W }{ m }\) |
||
| Symbol | English | Metric |
| \( T \) = Tension | \(lbf\) | \(N\) |
| \( W \) = Weight | \(lbf\) | \(N\) |
| \( m \) = Mass | \(lbm\) | \(kg\) |
| \( a \) = Acceleration | \(ft \;/\; sec^2\) | \(m \;/\; s^2\) |
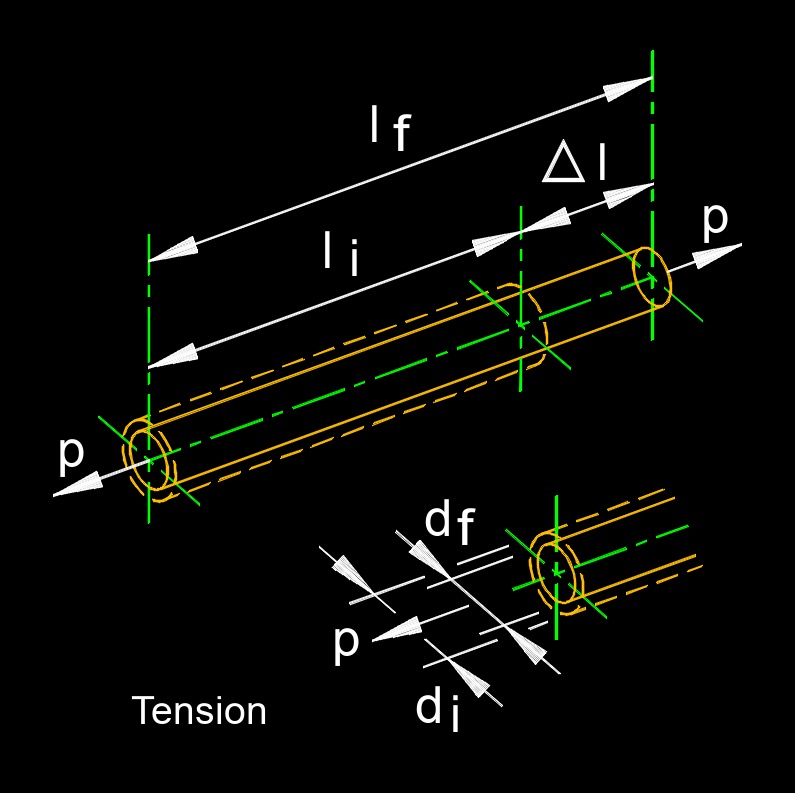Tension, abbreviated as T, is the force that is transmitted through a flexible or stretched object when it is pulled or stretched. It is a type of force that acts along the length of the object and is responsible for maintaining its shape and integrity.
Tension can be observed in various contexts, such as ropes, cables, strings, or elastic materials. When an external force is applied to one end of a flexible object, it creates tension that is transmitted throughout the object. This tension force acts in opposite directions along the length of the object, pulling the object's molecules or particles apart.
Tension Formula |
||
|
\( T \;=\; m \cdot g + m \cdot a \) (Tension) \( m \;=\; \dfrac{ T }{ g + a }\) \( g \;=\; \dfrac{ T }{ m } - a \) \( a \;=\; \dfrac{ T }{ m } - g \) |
||
| Symbol | English | Metric |
| \( T \) = Tension | \(lbf\) | \(N\) |
| \( m \) = Mass | \(lbm\) | \(kg\) |
| \( g \) = Gravitational Acceleration | \(ft \;/\; sec^2\) | \(m \;/\; s^2\) |
| \( a \) = Acceleration | \(ft \;/\; sec^2\) | \(m \;/\; s^2\) |
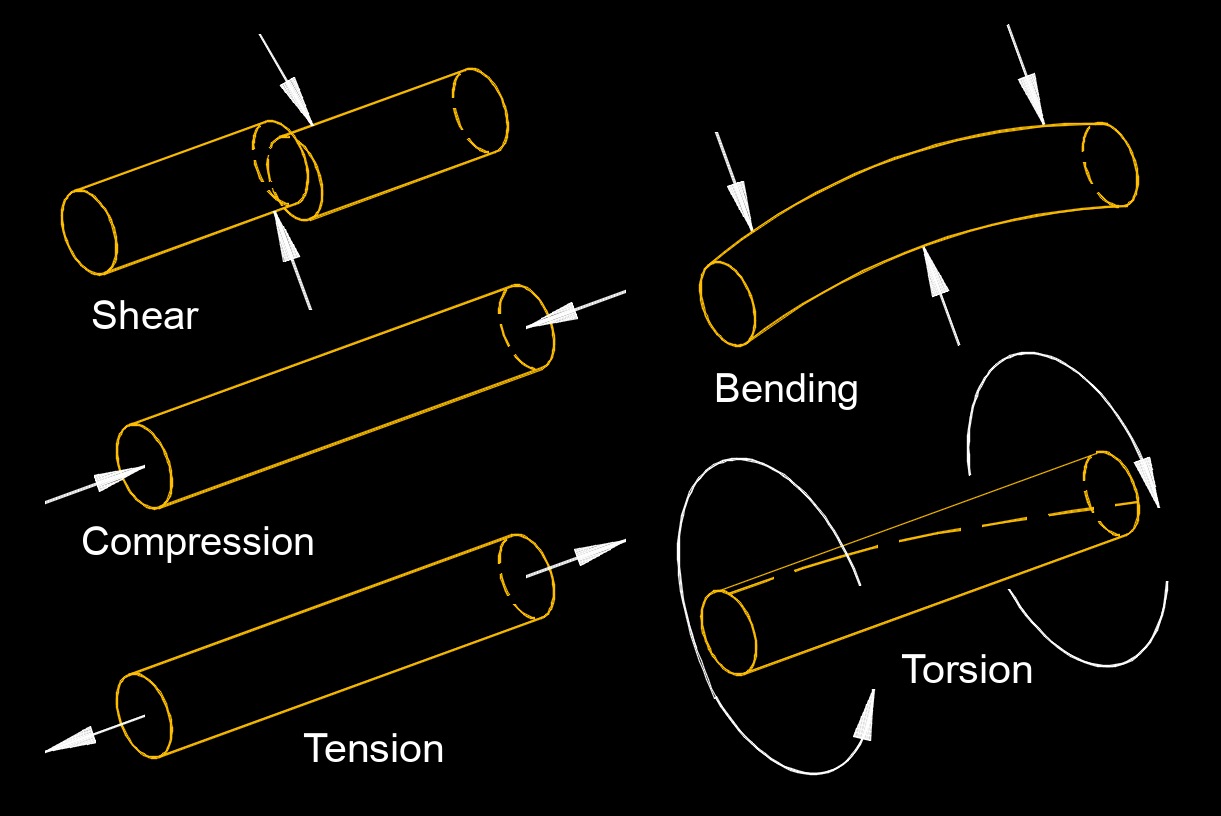
In a perfectly taut or idealized scenario, the tension force in a flexible object is uniform throughout its length. However, in real world situations, factors such as the weight of the object, variations in material properties, or the presence of external forces can cause variations in tension along the object's length. It's important to note that tension is distinct from compression, which is the force that acts to squeeze or compress an object. While tension acts to stretch or pull an object, compression acts to compress or push it together.
