Hydraulic Gradient
hydraulic gradient Formula |
||
|
\( i \;=\; \dfrac{ h_1 - h_2 }{ L }\) (Hydraulic Gradient) \( h_1 \;=\; i \cdot L + h_2 \) \( h_2 \;=\; h_1 - i \cdot L \) \( L \;=\; \dfrac{ h_1 - h_2 }{ i }\) |
||
| Symbol | English | Metric |
| \( i \) = Hydraulic Gradient | \(dimensionless\) | \(dimensionless\) |
| \( h_1 \) = Pressure Head at Point 1 | \(lbf \;/\; in^2\) | \(Pa\) |
| \( h_2 \) = Pressure Head at Point 2 | \(lbf \;/\; in^2\) | \(Pa\) |
| \( L \) = Horizontal Length of Column | \(ft\) | \(m\) |
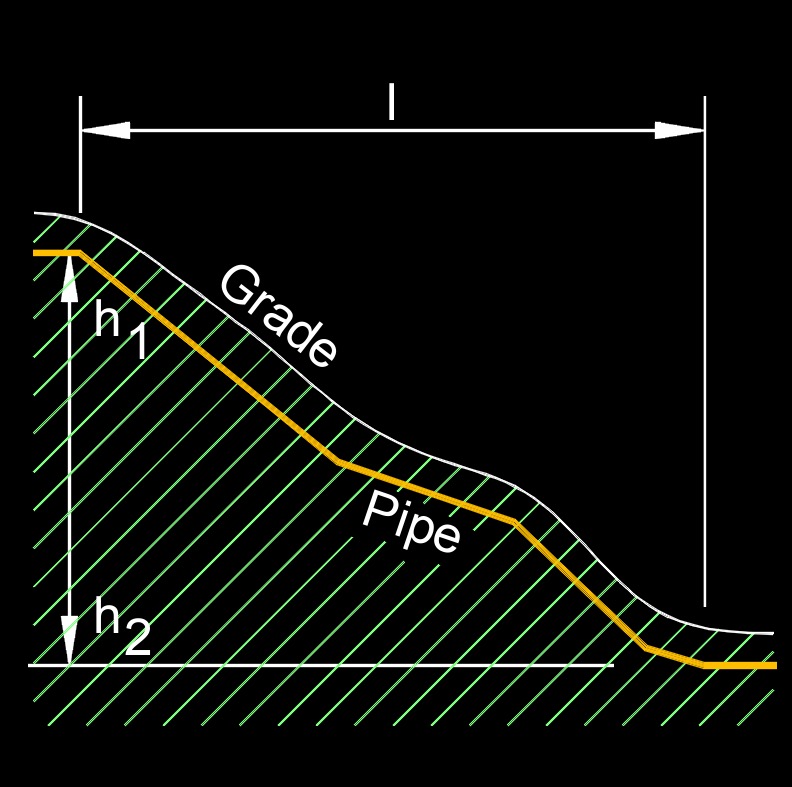
Hydraulic gradient, abbreviated as \(i\), also called hydraulic slope or energy gradient, a dimensionless number, is the change in height (pressure) to length between any two points. Or you could say the change in hydraulic head per unit distance along a flow path in a fluid system. It represents the driving force behind fluid flow and provides information about the direction and magnitude of flow within the system.
Hydraulic head is a measure of the total energy of a fluid at a specific point and is composed of two components, elevation head and pressure head. Elevation head is the potential energy due to the height of the fluid above a reference point, while pressure head is the energy associated with the pressure of the fluid at that point.
The hydraulic gradient represents the change in hydraulic head per unit of distance traveled along the flow path. The hydraulic gradient plays a crucial role in determining the direction and rate of fluid flow. Fluids tend to flow from regions of higher hydraulic head to regions of lower hydraulic head, following the path of steepest descent. The steeper the hydraulic gradient, the greater the driving force for flow.
In the context of groundwater flow, the hydraulic gradient is often used to describe the slope or inclination of the water table or the flow direction within an aquifer. It helps in understanding the movement of groundwater and can be used to estimate flow rates, travel times, and the overall behavior of the groundwater system. It's important to note that the hydraulic gradient assumes steady state flow conditions and does not take into account factors such as fluid viscosity, flow resistance, or the presence of obstacles or boundaries that may affect the actual flow behavior.

