Electric Current Density Formula |
||
|
\( J \;=\; \dfrac{ I }{ A_c }\) (Electric Current Density) \( I \;=\; J \cdot A_c \) \( A_c \;=\; \dfrac{ I }{ J }\) |
||
| Symbol | English | Metric |
| \( J \) = Electric Current Density | - | \(A \;/\; m^2\) |
| \( I \) = Current Through the Conductor | - | \(C \;/\; s\) |
| \( A_c \) = Area Cross-section of the Conductor | - | \(m^2\) |
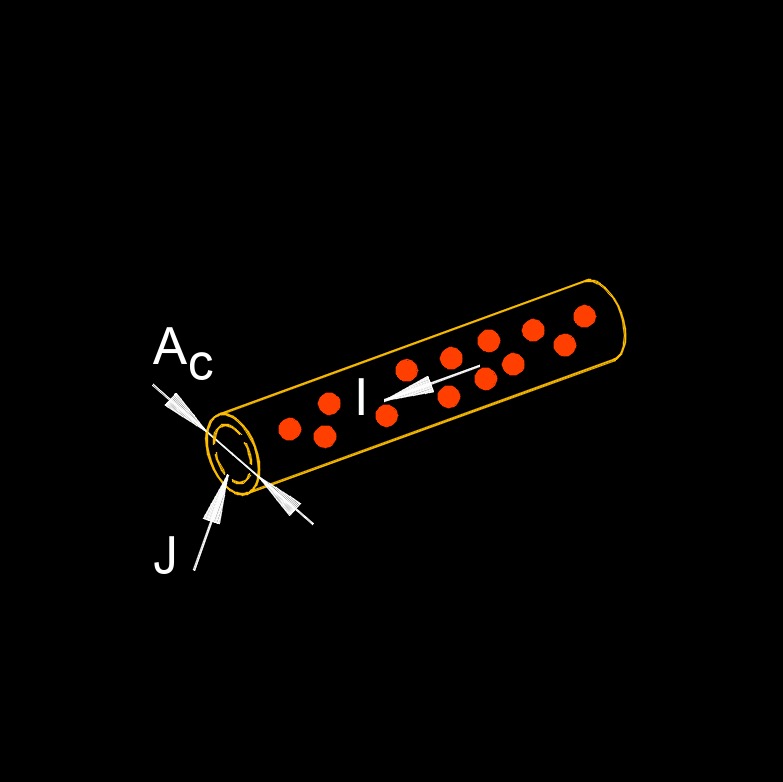Electric current density, abbreviated as J, refers to the amount of electric current flowing through a unit area of a conductor. It is a measure of the current per unit area cross-section and provides information about the distribution of electric current within a material. Current density is a vector quantity, meaning it has both magnitude and direction. Its direction is parallel to the direction of the flow of electric charge carriers (typically electrons) within the conductor.
Electric Current Density Formula |
||
|
\( J \;=\; \dfrac{ E }{ \sigma }\) (Electric Current Density) \( E \;=\; J \cdot \sigma \) \( \sigma \;=\; \dfrac{ E }{ J }\) |
||
| Symbol | English | Metric |
| \( J \) = Electric Current Density | - | \(A \;/\; m^2\) |
| \( E \) = Electric Field | - | \(V \;/\; m\) |
| \( \sigma \) (Greek symbol sigma) = Conductivity | - | \(S \;/\; m\) |
Current density is an important parameter in the analysis of electric circuits and the behavior of materials under the flow of electric current. It helps in understanding the distribution of current within conductors and the potential for localized heating or resistive losses. In materials with non-uniform area cross-sections, current density provides insights into the variations in current flow and can be used to assess the current carrying capacity of different sections.
In addition to its applications in electrical engineering, current density is also relevant in fields such as electrochemistry, semiconductor physics, and materials science, where the movement of electric charge plays a significant role.
