Magnetic Flux Density

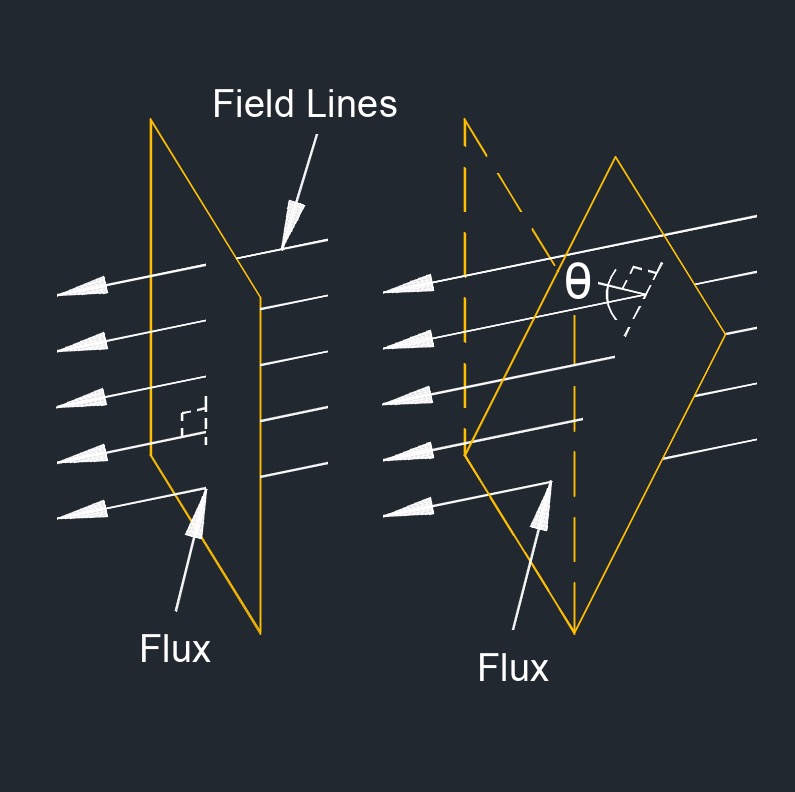
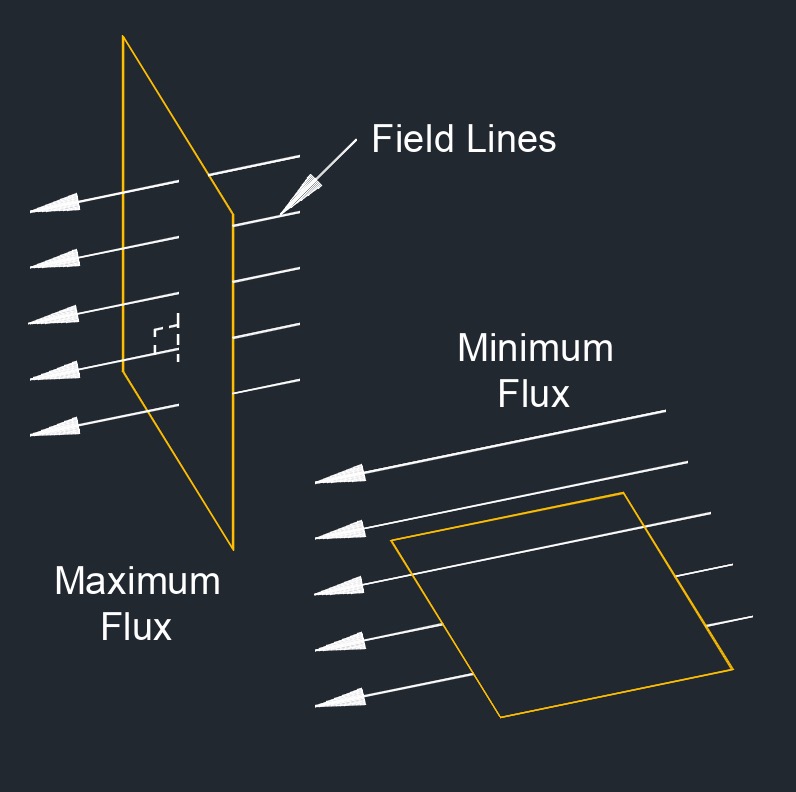
Magnetic flux density, abbreviated as , also called flux density, is a measure of the strength and direction of a magnetic field.  It quantifies the amount of magnetic flux per unit area perpendicular to the magnetic field.  It represents how concentrated the magnetic field lines are within a given region of space.  The magnetic flux density at a specific point in space is defined as the force experienced by a unit magnetic pole placed at that point, divided by the product of the pole's strength and the area it occupies. 

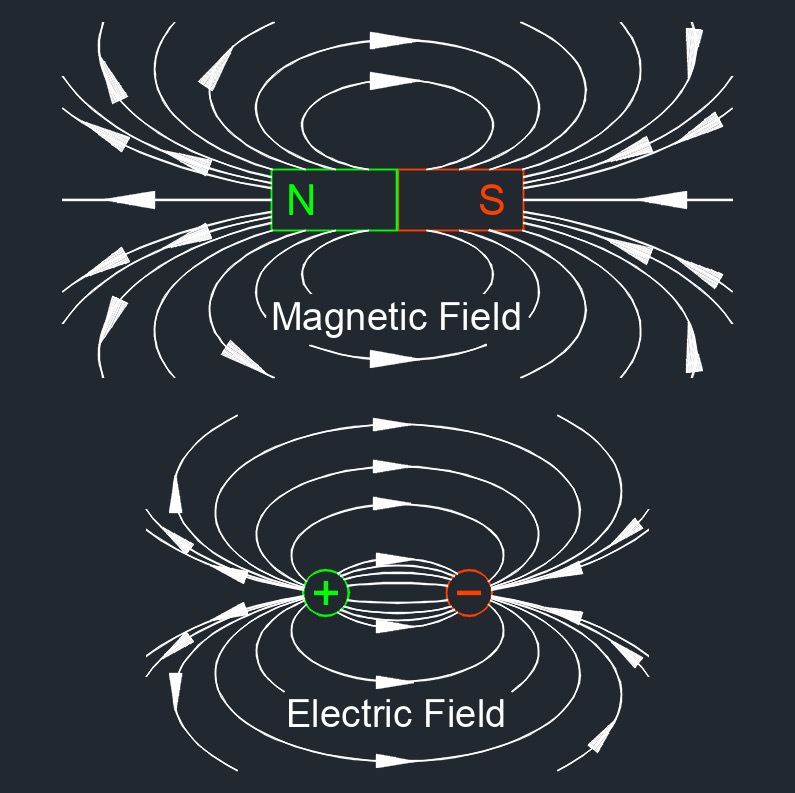Magnetic flux density is a vector quantity, meaning it has both magnitude and direction.  It is used in various applications, including the design of electromagnets, magnetic materials, and devices such as electric motors and generators.  The strength of the magnetic field around a magnet or a current carrying conductor is directly proportional to the magnetic flux density.

 

Magnetic flux density formula
\( B  \;=\;  \Phi_B \;/\; A \)     (Magnetic Flux Density) \( \Phi_B  \;=\;  B \; A \) \( A  \;=\;  \Phi_B \;/\; B \)
Symbol	English	Metric
\( B \) = Magnetic Flux Density	-	\(T\)
\( \Phi_B \)  (Greek symbol Phi) = Magnetic Flux	-	\(Wb \;/\; mm^2\)
\( A \) = Area Cross-section Perpendicular to Magnetic Field B	-	\(m^2\)

   

Magnetic flux density formula
\( B \;=\; F \;/\; n \; I \; L \)     (Magnetic Flux Density) \( F \;=\; B \; n \; I \; L \) \( n \;=\; F \;/\; B \; I \; L \) \( I \;=\; F \;/\; B \; n \; L \) \( L \;=\; F \;/\; B \; n \; I \)
Symbol	English	Metric
\( B \) = Magnetic Flux Density	-	\(T\)
\( F \) = Current Force	-	\(N\)
\( n \) = Number of the Wires Carrying the Current	-	\(dimensionless\)
\( I \) = Current	-	\(C\;/\;s\)
\( L \) = Length of the Current Carrying Wire in the Field	-	\(m\)