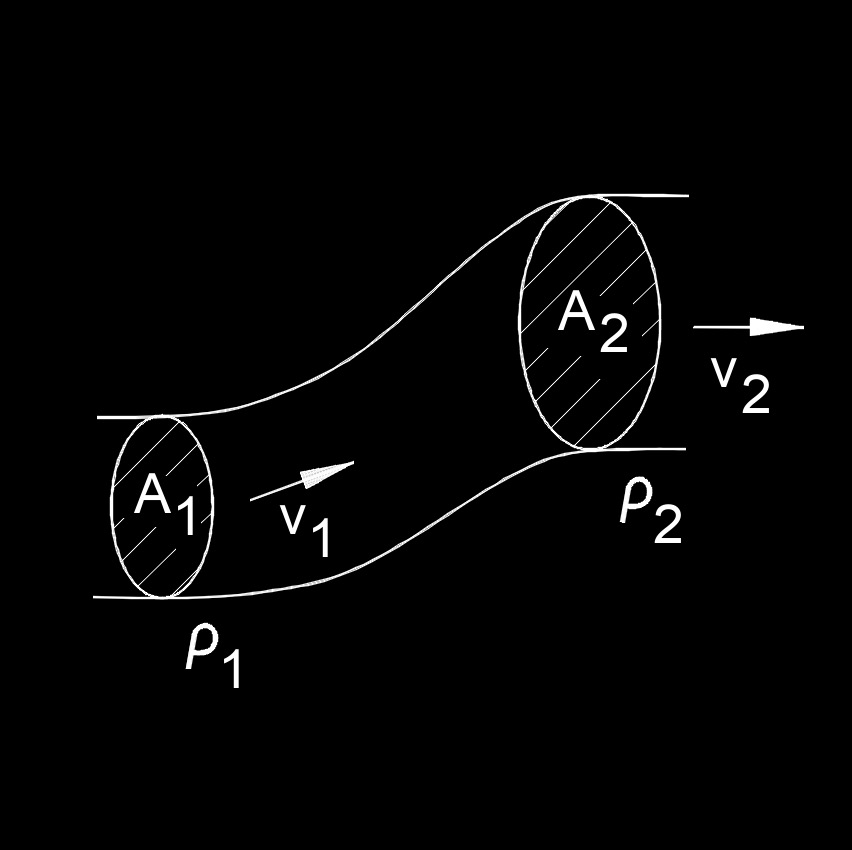
Continuity Equation for Area
Continuity equation is the moving of a quantity through a pipe in a steady flow. This formula calculates the initial cross-section area of the pipe.
Continuity Equation for Area Formula
|
||
|
\( A_1 \;=\; \dfrac{ \rho_2 \cdot A_2 \cdot v_2 }{ v_1 \cdot \rho_1 }\) (Continuity Equation for Area) \( \rho_2 \;=\; \dfrac{ A_1 \cdot v_1 \cdot \rho_1 }{ A_2 \cdot v_2 }\) \( A_2 \;=\; \dfrac{ A_1 \cdot v_1 \cdot \rho_1 }{ \rho_2 \cdot v_2 }\) \( v_2 \;=\; \dfrac{ A_1 \cdot v_1 \cdot \rho_1 }{ \rho_2 \cdot A_2 }\) \( v_1 \;=\; \dfrac{ \rho_2 \cdot A_2 \cdot v_2 }{ A_1 \cdot \rho_1 }\) \( \rho_1 \;=\; \dfrac{ \rho_2 \cdot A_2 \cdot v_2 }{ A_1 \cdot v_1 }\) |
||
| Symbol | English | Metric |
| \( A_1 \) = Initial Area Cross-section | \(in^2\) | \(mm^2\) |
| \( \rho_2 \) (Greek symbol rho) = Final Cross-section Density | \(lbm \;/\; ft^3\) | \(kg \;/\; m^3\) |
| \( A_2 \) = Final Area Cross-section | \(in^2\) | \(mm^2\) |
| \( v_2 \) = Final Area Cross-section Velocity | \(ft \;/\; sec\) | \(m \;/\; s\) |
| \( v_1 \) = Initial Area Cross-section Velocity | \(ft \;/\; sec\) | \(m \;/\; s\) |
| \( \rho_1 \) (Greek symbol rho) = Initial Area Cross-section Density | \(lbm \;/\; ft^3\) | \(kg \;/\; m^3\) |
