Coriolis Acceleration Formula |
||
|
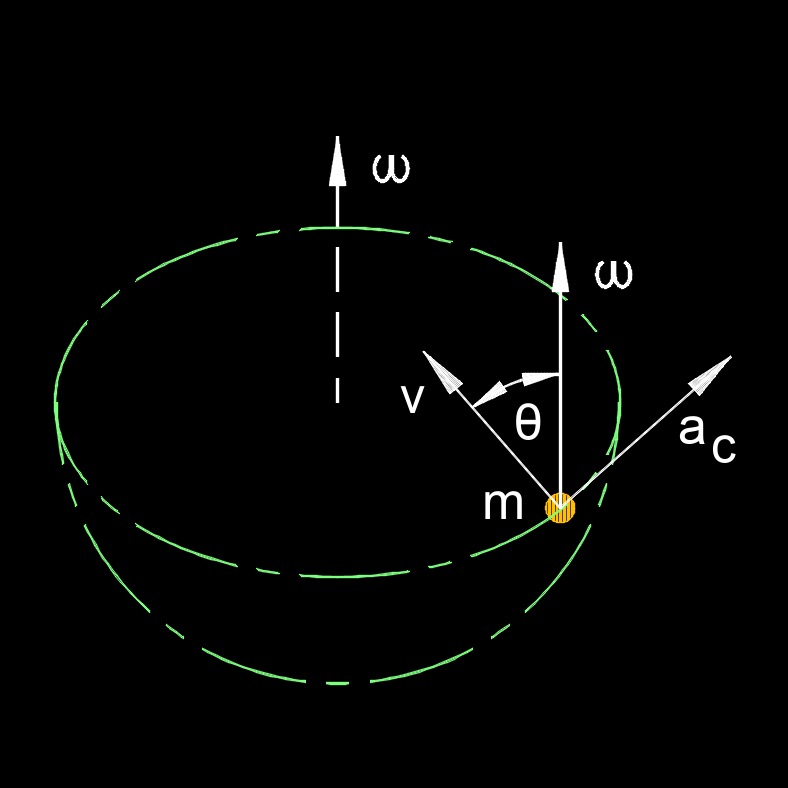
\( a_c \;=\; 2 \cdot v \cdot \omega \cdot sin( \theta) \) (Coriolis Acceleration) \( v \;=\; \dfrac{ a_c }{ 2 \cdot \omega \cdot sin( \theta) } \) \( \omega \;=\; \dfrac{ a_c }{ 2 \cdot v \cdot sin( \theta) } \) \( sin( \theta) \;=\; \dfrac{ a_c }{ 2 \cdot v \cdot \omega } \) |
||
| Symbol | English | Metric |
| \( a_c \) = Coriolis Acceleration | \(ft \;/\; sec^2\) | \(m \;/\; s^2\) |
| \( v \) = Velocity | \(ft \;/\; sec\) | \(m \;/\; s\) |
| \( \omega \) (Greek symbol omega) = Angular Velocity | \(deg \;/\; sec\) | \(rad \;/\; sec\) |
| \( \theta \) (Greek symbol theta) = Angle | \(deg\) | \(rad\) |
Coriolis acceleration, abbreviated as \(a_c\), also called Coriolis effect or Coriolis force, is an apparent force that appears to act on objects moving in a rotating reference frame, such as the Earth. This effect is a consequence of the conservation of angular momentum and the fact that different points on a rotating object have different linear velocities.
In other terms, when an object or fluid moves within a rotating system (like the Earth's rotation), it appears to experience a deflection or acceleration that is perpendicular to its velocity. This deflection is to the right in the northern hemisphere and to the left in the southern hemisphere. The Coriolis acceleration is responsible for many observable phenomena, including the rotation of weather systems (such as cyclones and anticyclones), the curved paths of ocean currents, and the direction of airflow in the atmosphere.
The Coriolis acceleration is responsible for the curved paths of moving objects in a rotating system and has important implications in various fields, including meteorology, oceanography, and engineering. It's a fundamental concept for understanding the behavior of objects and fluids on a rotating planet like Earth.
