Apothem
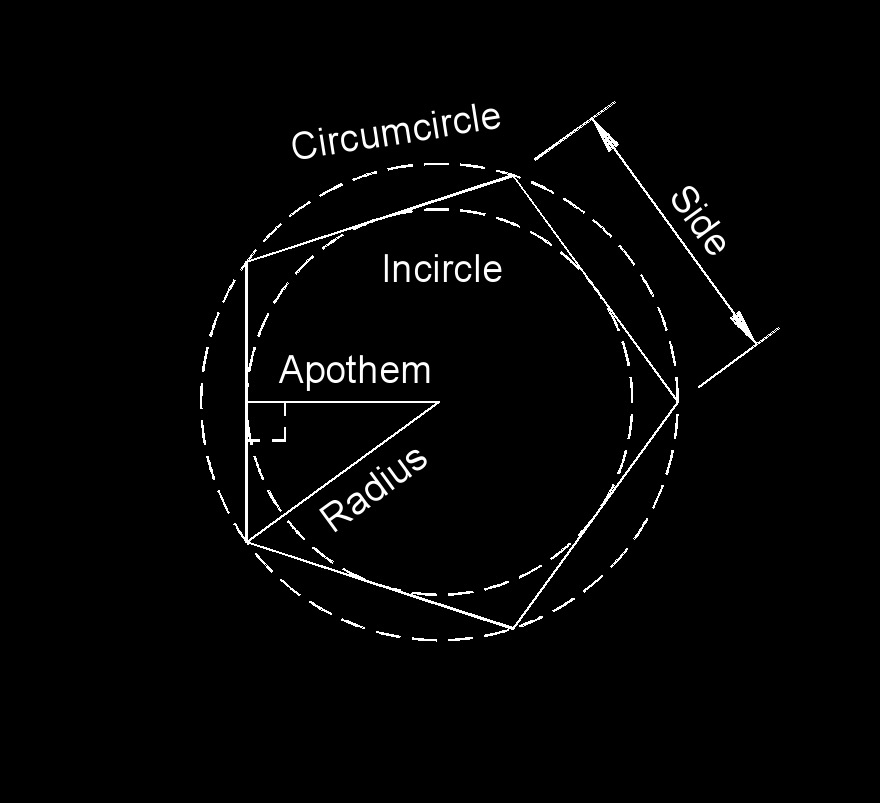 Apothem is the length of a line perpendicular from the center to the midpoint of the side of a regular polygon.
Apothem is the length of a line perpendicular from the center to the midpoint of the side of a regular polygon.- A irregular polygon has no center so there can be no apothem.
Apothem Edge formula |
||
| \(\large{A=\frac {s} {2 \;tan\; \left( \frac{180}{n} \right) } }\) | ||
| Symbol | English | Metric |
| \(\large{A}\) = apothem | \(\large{in}\) | \(\large{mm}\) |
| \(\large{s}\) = edge (side length) | \(\large{in}\) | \(\large{mm}\) |
| \(\large{n}\) = number of sides | \(\large{dimensionless}\) | |
| \(\large{tan}\) = tangent | \(\large{deg}\) | \(\large{rad}\) |
Apothem Radius formula |
||
| \(\large{A= r \;cos\; {\left( \frac{180}{n} \right) } }\) | ||
| Symbol | English | Metric |
| \(\large{A}\) = apothem | \(\large{in}\) | \(\large{mm}\) |
| \(\large{cos}\) = cosine | \(\large{deg}\) | \(\large{rad}\) |
| \(\large{n}\) = number of sides | \(\large{dimensionless}\) | |
| \(\large{r}\) = radius | \(\large{in}\) | \(\large{mm}\) |

