Angular Momentum for a Point Particle Formula |
||
| \( L \;=\; r \;x\; p \) | ||
| Symbol | English | Metric |
| \( L \) = Angular Momentum | \(lbm - ft^2 \;/\; sec\) | \(kg - m^2 \;/\; s\) |
| \( r \) = Position Vector from the Axis of Rotation to the Particle | \(ft\) | \(m\) |
| \( x \) = Cross Product | - | - |
| \( p \) = Linear Momentum | \(lbm - ft \;/\; sec\) | \(kg - m \;/\; s\) |
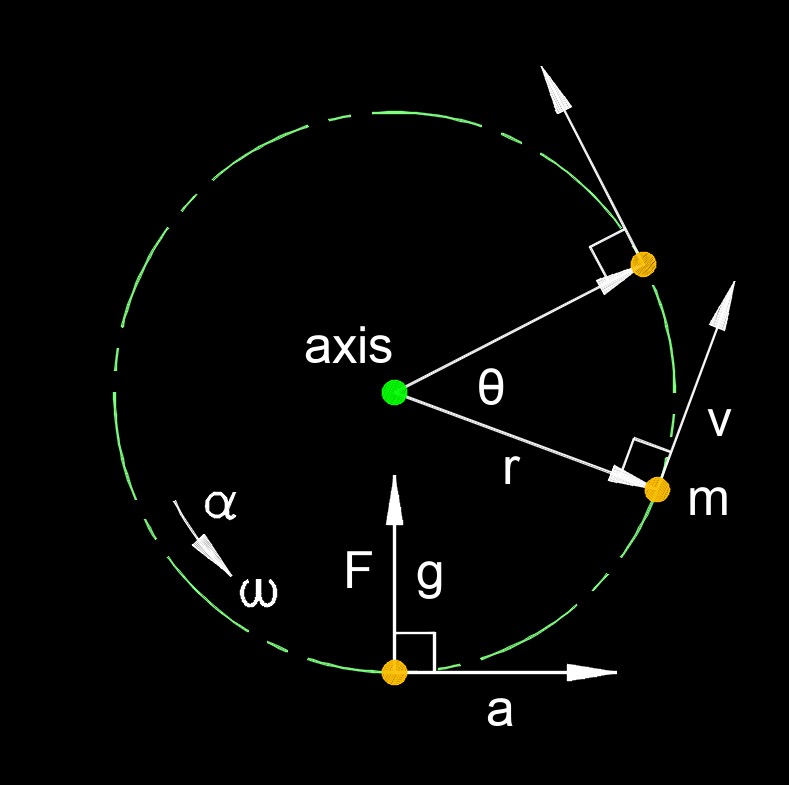Angular momentum for a point particle is a physical quantity that captures the rotational motion of the particle about a specific point or axis, defined as the cross product of its position vector and its linear momentum. The magnitude of angular momentum depends on the particle’s mass, its speed, the distance from the axis of rotation, and the angle between the position and velocity vectors. This vector quantity has both magnitude and direction, with the direction determined by the right-hand rule, perpendicular to the plane formed by r and p. Angular momentum is conserved when no external torques act on the particle, a principle that explains behaviors like the orbital motion of planets or satellites. This concept is crucial in both classical and quantum mechanics for analyzing rotational dynamics.
