Ideal Gas Law Density Formula |
||
|
\( \rho \;=\; \dfrac{ p }{ R \cdot T }\) (Ideal Gas Law Density) \( p \;=\; \rho \cdot R \cdot T \) \( R \;=\; \dfrac{ p }{ \rho \cdot T }\) \( T \;=\; \dfrac{ p }{ \rho \cdot R }\) |
||
| Symbol | English | Metric |
| \( \rho \) (Greek symbol rho) = density of gas | \(lbm\;/\;ft^3\) | \(kg\;/\;m^3\) |
| \( p \) = pressure | \(lbf\;/\;in^2\) | \(Pa\) |
| \( R \) = specific gas constant (gas constant) | \(ft-lbf\;/\;lbm-R\) | \(J\;/\;kg-K\) |
| \( T \) = temperature | \( R \) | \(K \) |
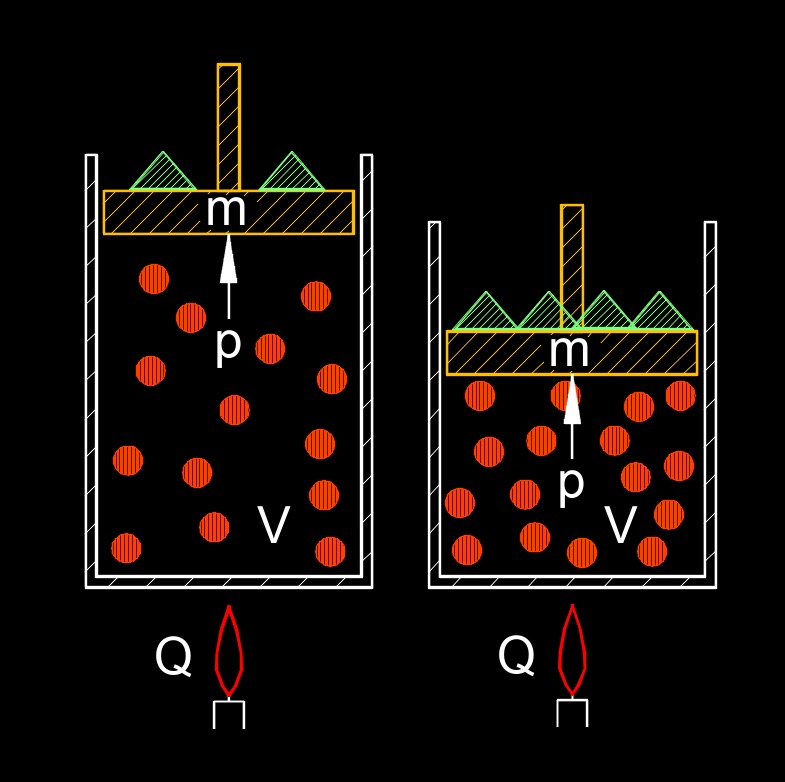
The ideal gas law, expressed as PV=nRT, can be manipulated to express the density of a gas. Density is defined as mass per unit volume.. We can relate mass to the number of moles using the molar mass of the gas. This form of the ideal gas law shows that the density of a gas is directly proportional to its pressure and molar mass, and inversely proportional to its absolute temperature. Therefore, for a given gas, increasing the pressure or decreasing the temperature will lead to a higher density, while increasing the temperature or decreasing the pressure will result in a lower density.
