Constant Head Permeability

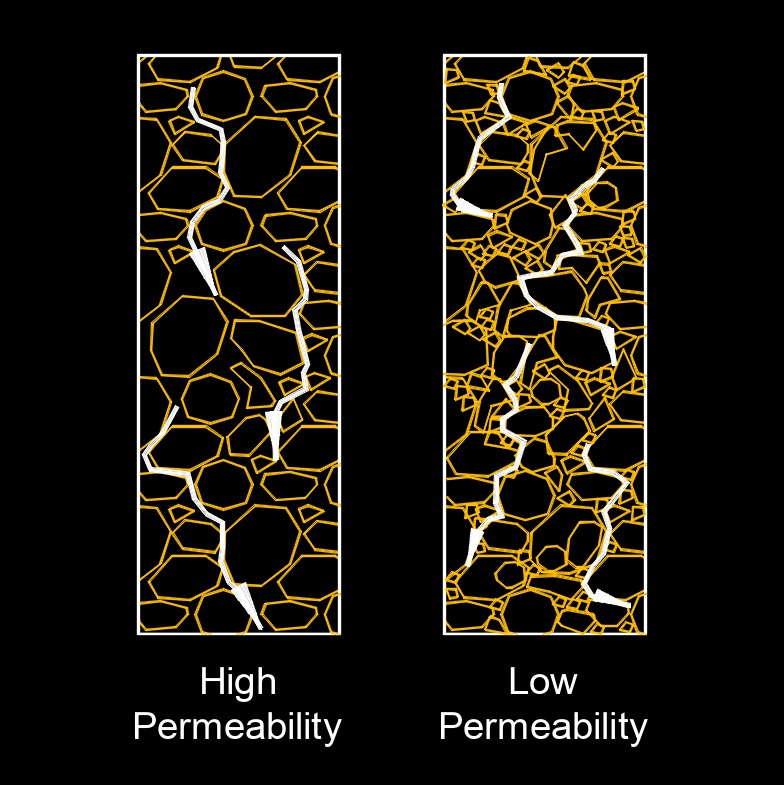Constant head permeability, abbreviated as \( k \), describe the ability of a porous material, such as soil or rock, to transmit fluids under constant hydraulic head conditions.  It is a measure of the ease with which water can flow through a porous medium and is an important parameter in understanding groundwater flow and the design of various engineering and environmental systems.

In a constant head permeability tests, a sample of the porous material is placed in a permeameter, which is typically a column or cylinder with a known cross-sectional area.  Water is allowed to flow through the sample, and the hydraulic head difference across the sample remains constant during the test.  By measuring the flow rate of water through the sample and the hydraulic head difference, the constant head permeability can be calculated using Darcy's law, which relates flow rate, hydraulic head, and hydraulic conductivity.

Constant head permeability is an essential parameter for assessing the suitability of a material for various applications, such as groundwater modeling, contaminant transport analysis, and the design of drainage systems, seepage control measures, and geotechnical engineering projects. 

 

Constant Head Permeability formula
\( k =  V_w\;l \;/\; A_c \; h \; t \)
Symbol	English	Metric
\( k \) = constant head permeability	\(ft^3\)	\(m^3\)
\( A_c \) = area cross-section of sample	\(ft^2\)	\(m^2\)
\( h \) = head causing flow	\(ft\)	\(m\)
\( l \) = length of sample	\(ft\)	\(m\)
\( t \) = time duration for collection of water	\(\large{sec}\)	\(\large{s}\)
\( V_w \) = volume of water collected	\(ft^3\)	\(m^3\)