- Article Link - Geometric Properties of Structural Shapes
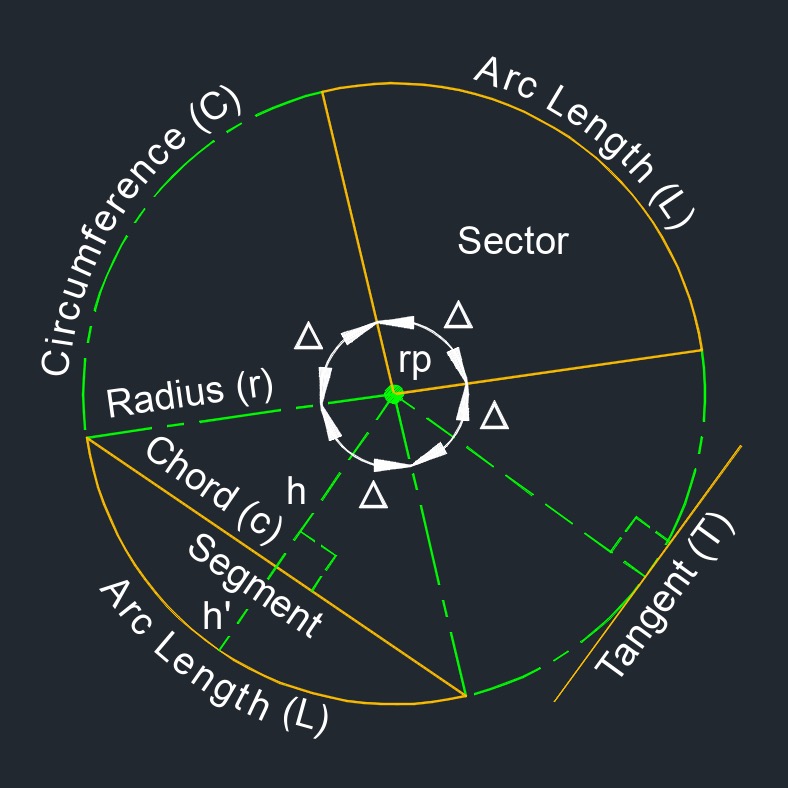
arc Length of a Quarter Circle formula |
||
| \( L \;=\; \dfrac{ 2 \cdot \pi \cdot r }{ 4 }\) | ||
| Symbol | English | Metric |
| \( L \) = arc length | \( in \) | \( mm \) |
| \( \pi \) = Pi | \(3.141 592 653 ...\) | \(3.141 592 653 ...\) |
| \( r \) = radius | \( in \) | \( mm \) |
- A part of the interior of a circle having two radius boundries at a 90° angle and an arc.
- Center of a circle having all points on the line circumference are at equal distance from the center point.
- A quarter circle is a structural shape used in construction.
area of a Quarter Circle formula |
||
| \( A \;=\; \dfrac{ \pi \cdot r^2 }{ 4 }\) | ||
| Symbol | English | Metric |
| \( A \) = area | \( in^2 \) | \( mm^2 \) |
| \( \pi \) = Pi | \(3.141 592 653 ...\) | \(3.141 592 653 ...\) |
| \( r \) = radius | \( in \) | \( mm \) |
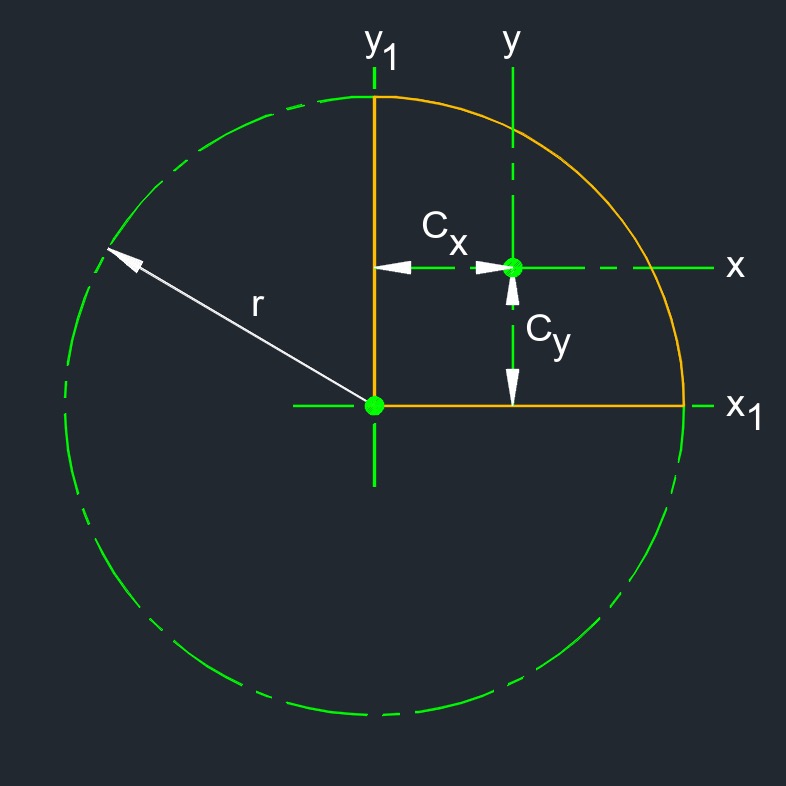
Distance from Centroid of a Quarter Circle formulas |
||
|
\( C_x \;=\; \dfrac{ 4 \cdot r }{ 3 \cdot \pi }\) \( C_y \;=\; \dfrac{ 4 \cdot r }{ 3 \cdot \pi }\) |
||
| Symbol | English | Metric |
| \( C_x, C_y \) = distance from centroid | \( in \) | \( mm \) |
| \( \pi \) = Pi | \(3.141 592 653 ...\) | \(3.141 592 653 ...\) |
| \( r \) = radius | \( in \) | \( mm \) |
Elastic Section Modulus of a Quarter Circle formula |
||
| \( S \;=\; \dfrac{ I_x }{ C_y }\) | ||
| Symbol | English | Metric |
| \( S \) = elastic section modulus | \(in^3\) | \(mm^3\) |
| \( I \) = moment of inertia | \(lbm\;/\;ft^2-sec\) | \(kg\;/\;m^2\) |
Perimeter of a Quarter Circle formulas |
||
|
\( P \;=\; \dfrac{ 2 \cdot \pi \cdot r }{ 4 } + 2 \cdot r \) \( P \;=\; L + 2 \cdot r \) |
||
| Symbol | English | Metric |
| \( P \) = perimeter | \( in \) | \( mm \) |
| \( L \) = arc length | \( in \) | \( mm \) |
| \( \pi \) = Pi | \(3.141 592 653 ...\) | \(3.141 592 653 ...\) |
| \( r \) = radius | \( in \) | \( mm \) |
Polar Moment of Inertia of a Circle formulas |
||
|
\( J_{z} \;=\; \left( \dfrac{ \pi }{ 8 } - \dfrac{ 8 }{ 9 \cdot \pi } \right) \cdot r^4 \) \( J_{z1} \;=\; \dfrac{ \pi \cdot r^4 }{ 8 }\) |
||
| Symbol | English | Metric |
| \( L \) = arc length | \( in \) | \( mm \) |
| \( \pi \) = Pi | \(3.141 592 653 ...\) | \(3.141 592 653 ...\) |
| \( r \) = radius | \( in \) | \( mm \) |
Radius of a Quarter Circle formula |
||
| \( r \;=\; \sqrt{ \dfrac{ 2 \cdot A }{ \pi } }\) | ||
| Symbol | English | Metric |
| \( r \) = radius | \( in \) | \( mm \) |
| \( A \) = area | \( in^2 \) | \( mm^2 \) |
| \( \pi \) = Pi | \(3.141 592 653 ...\) | \(3.141 592 653 ...\) |
Radius of Gyration of a Half Circle formulas |
||
|
\( k_{x} \;=\; r \cdot \sqrt{ \dfrac{ 1 }{ 4 } - \dfrac{ 16 }{ 9 \cdot \pi^2} } \) \( k_{y} \;=\; r \cdot \sqrt{ \dfrac{ 1 }{ 4 } - \dfrac{ 16 }{ 9 \cdot \pi^2} } \) \( k_{z} \;=\; r \cdot \sqrt{ \dfrac{ 1 }{ 2 } - \dfrac{ 16 }{ 9 \cdot \pi^2} } \) \( k_{x1} \;=\; \dfrac{ r }{ 2 } \) \( k_{y1} \;=\; \dfrac{ r }{ 2 } \) \( k_{z1} \;=\; \dfrac{ \sqrt {2} }{ 2 } \cdot r \) |
||
| Symbol | English | Metric |
| \( k \) = radius of gyration | \( in \) | \( mm \) |
| \( \pi \) = Pi | \(3.141 592 653 ...\) | \(3.141 592 653 ...\) |
| \( r \) = radius | \( in \) | \( mm \) |
Second Moment of Area of a Half circle formulas |
||
|
\( I_{x} \;=\; \left( \dfrac{ \pi }{ 16 } - \dfrac{ 4 }{ 9 \cdot \pi } \right) \cdot r^4 \) \( I_{y} \;=\; \left( \dfrac{ \pi }{ 16 } - \dfrac{ 4 }{ 9 \cdot \pi } \right) \cdot r^4 \) \( I_{x1} \;=\; \dfrac{ \pi \cdot r^4}{ 16 }\) \( I_{y1} \;=\; \dfrac{ \pi \cdot r^4}{ 8 }\) |
||
| Symbol | English | Metric |
| \( I \) = moment of inertia | \( in^4 \) | \( mm^4 \) |
| \( \pi \) = Pi | \(3.141 592 653 ...\) | \(3.141 592 653 ...\) |
| \( r \) = radius | \( in \) | \( mm \) |