Regular Polygon

• Regular polygon (a two-dimensional figure) is a polygon where all sides are congruent and all angles are congruent.
• Circumcircle is a circle that passes through all the vertices of a two-dimensional figure.
• Congruent is all sides having the same lengths and angles measure the same.
• Inscribed circle is the largest circle possible that can fit on the inside of a two-dimensional figure.
• Polygon (a two-dimensional figure) is a closed plane figure for which all sides are line segments and not necessarly congruent.

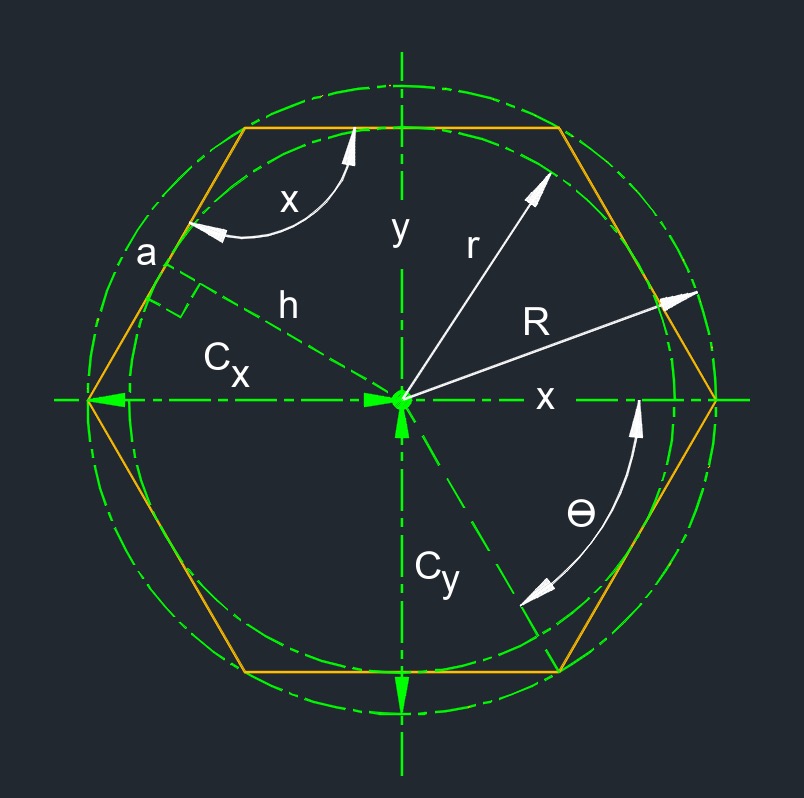• See Artical Links  -  Geometric Properties of Structural Shapes
• Tags: Structural Steel

Regular Polygon Index

• Regular Polygon Types
• Area of a Regular Polygon
• Central Angle of a Regular Polygon
• Circumcircle Radius of a Regular Polygon
• Distance from Centroid of a Polygon
• Edge of a Regular Polygon
• Elastic Section Modulus of a Polygon
• Inscribed Radius of a Regular Polygon
• Number of Diagonals of a Regular Polygon
• Perimeter of a Regular Polygon
• Polar Moment of Inertia of a Polygon
• Radius of Gyration of a Polygon
• Second Moment of Area of a Rectangle
  

Regular Polygon Types

• Triangle - 3 sides - 60° interior angle
• Quadrilateral - 4 sides - 90° interior angle
• Pentagon - 5 sides - 108° interior angle
• Hexagon - 6 sides - 120° interior angle
• Heptagon - 7 sides - 128.571° interior angle
• Octagon - 8 sides - 135° interior angle
• Nonagon - 9 sides - 140° interior angle
• Decagon - 10 sides - 144° interior angle
• Hendecagon - 11 sides - 147.273° interior angle
• Dodecagon - 12 sides - 150° interior angle
• Triskaidecagon - 13 sides - 152.308° interior angle
• Tetrakaidecagon - 14 sides - 154.286° interior angle
• Pentadecagon - 15 sides - 156° interior angle
• Hexakaidecagon - 16 sides - 157.5° interior angle
• Heptadecagon - 17 sides - 158.824° interior angle
• Octakaidecagon - 18 sides - 160° interior angle
• Enneadecagon - 19 sides - 161.053° interior angle
• Icosagon - 20 sides - 162° interior angle

 

area of a Regular Polygon formulas
\( A_{area} \;=\;  a^2 \; n\;/\;4 \; tan( \frac{180}{n} )    \) \( A_{area} \;=\; R^2 \; n \; sin( \frac{360}{n} )   \;/\;2  \) \( A_{area} \;=\; r^2 \; n \; tan( \frac{180}{n} )  \) \( A_{area} \;=\; \frac{1}{4} \; a^2 \; n \; cot( \frac{\pi}{n} )  \)
Symbol	English	Metric
\( A_{area} \) = area	\( in^2 \)	\( mm^2 \)
\( a \) = edge	\( in \)	\( mm \)
\( r \) = inside radius (apothem)	\( in \)	\( mm \)
\( n \) = number of edges	\( dimensionless \)
\( R \) = outside radius	\( in \)	\( mm \)
\( P \) = perimeter	\( in \)	\( mm \)

 

Central Angle of a Regular Polygon formulaCE
\( CA \;=\; 360\;/\;n \)
Symbol	English	Metric
\( CA \) = central angle	\( deg \)	\( rad \)
\( n \) = number of edges	\( dimensionless \)

 

Circumcircle Radius of a Regular Polygon formula
\( R \;=\; a\;/\;2 \; sin( \frac{180}{n} )  \)
Symbol	English	Metric
\( R \) = outside radius	\( in \)	\( mm \)
\( a \) = edge	\( in \)	\( mm \)
\( n \) = number of edges	\( dimensionless \)

 

Distance from Centroid of a Polygon formulas
\( C_x \;=\; R  \) \( C_y \;=\; R  \)
Symbol	English	Metric
\( C \) = distance from centroid	\( in \)	\( mm \)
\( R \) = outside radius	\( in \)	\( mm \)

 

Edge of a Regular Polygon formulas
\( a \;=\; 2 \;r \; tan( \frac{180}{n} )  \) \( a \;=\; 2 \; R \; sin( \frac{180}{n} )   \)
Symbol	English	Metric
\( a \) = edge	\( in \)	\( mm \)
\( r \) = inside radius (apothem)	\( in \)	\( mm \)
\( R \) = outside radius	\( in \)	\( mm \)

 

Elastic Section Modulus of a Polygon formula
\( S \;=\; I_x \;/\; R \)
Symbol	English	Metric
\( S \) = elastic section modulus	\( in^3 \)	\( mm^3 \)
\( I \) = moment of inertia	\( in^4 \)	\( mm^4 \)
\( R \) = outside radius	\( in \)	\( mm \)

 

Inscribed Radius of a Regular Polygon formulas
\(  r \;=\; a \;/\; 2\; tan( \frac{180}{n} )  \)  \(  r \;=\; R \; cos( \frac{180}{n} )   \)
Symbol	English	Metric
\( r \) = inside radius (apothem)	\( in \)	\( mm \)
\( a \) = edge	\( in \)	\( mm \)
\( n \) = number of edges	\( dimensionless \)
\( R \) = outside radius	\( in \)	\( mm \)

 

Number of Diagonals of a Regular Polygon formula
\( D' \;=\; n \; ( n - 3 )  \;/\;2 \)
Symbol	English	Metric
\( D' \) = diagonal	\( in \)	\( mm \)
\( a \) = edge	\( in \)	\( mm \)
\( n \) = number of edges	\( dimensionless \)

   

Perimeter of a Regular Polygon formula
\( P \;=\; a \; n  \)
Symbol	English	Metric
\( P \) = perimeter	\( in \)	\( mm \)
\( a \) = edge	\( in \)	\( mm \)
\( n \) = number of edges	\( dimensionless \)

 

Polar Moment of Inertia of a Polygon formula
\( J_{z} \;=\; 2 \; A \; ( 6 \; R^2 - a^2 \;/\;24 ) \)
Symbol	English	Metric
\( J \) = torsional constant	\( in^4 \)	\( mm^4 \)
\( a \) = edge	\( in \)	\( mm \)
\( R \) = outside radius	\( in \)	\( mm \)

 

Radius of Gyration of a Polygon formulas
\( k_{x} \;=\;   \sqrt{  6 \; R^2 - a^2 \;/\;24  }    \)  \( k_{y} \;=\;   \sqrt{  6 \; R^2 - a^2 \;/\;24  }   \)  \( k_{z} \;=\;   \sqrt{  k_{x}{^2}  +  k_{y}{^2}  }   \)
Symbol	English	Metric
\( k \) = radius of gyration	\( in \)	\( mm \)
\( a \) = edge	\( in \)	\( mm \)
\( R \) = outside radius	\( in \)	\( mm \)

 

Second Moment of Area of a Rectangle formulas
\( I_{x} \;=\; 2 \; A \; (  6 \; R^2 - a^2 \;/\;24 )  \)  \( I_{y} \;=\; 2 \; A \; (  6 \; R^2 - a^2 \;/\;24 )  \)
Symbol	English	Metric
\( I \) = moment of inertia	\( in^4 \)	\( mm^4 \)
\( a \) = edge	\( in \)	\( mm \)
\( R \) = outside radius	\( in \)	\( mm \)