Force Exerted by Contracting or Stretching a Material

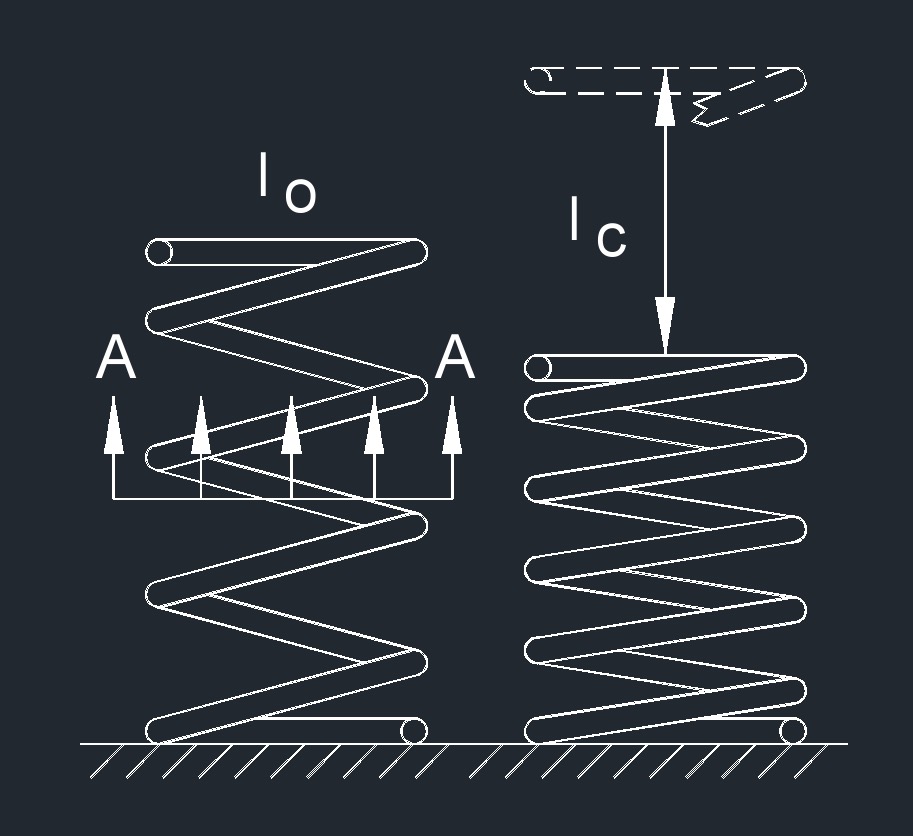Any strain exerted on a material causes an internal elastic stress.  The force applied on a material when contracting or stretching is related to how much the length of the object changes.

 

Force Exerted by Contracting or Stretching a Material formula

\(\large{ F =    \frac { \lambda \;A\; l_c  } { l_o  }  }\)

Where:

\(\large{ F }\) = force exerted

\(\large{ l_c }\) = change in length

\(\large{ l_o }\) = origional length

\(\large{ \lambda }\)  (Greek symbol lambda) = modulus of elasticity

\(\large{ A }\) = origional area cross-section through which the force is applied