Stress

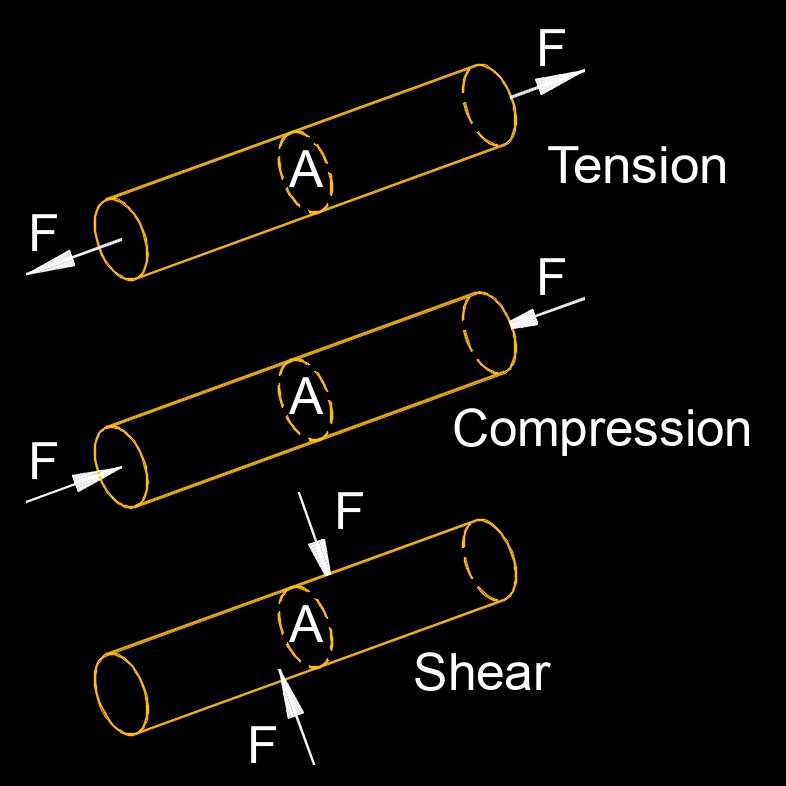
Stress, abbreviated as \(\sigma \) (Greek symbol sigma), also called normal stress, is the force per unit area of cross-section.  The maximum stress of a material before it breaks is called breaking stress or ultimate tensial stress.

 

Stress Types

• Bulk Stress (Volume Stress)  -  The volume of the body changes due to the stress.

• Compressive Stress  -  The opposite of tensile stress.

• Cylinder Hoop Stress  -  The circumference stress in a cylinder of pipe having both ends closed due to internal pressure.

• Fatigue Stress  -  Failure or weakening of a material due to repetition and load cycling.

• Flow Stress  -  When a mass of flowing fluid indicates a dynamic pressure on a conduit wall.

• Hoop Stress  -  The circumferential and perpendicular stress to the axis imposed on a cylinder wall when exposed to an internal pressure load.

• Hydraulic Stress  -  The internal force per unit area when the force is applied by the fluid on the body.

• Longitudinal Stress  - When the length of the body changes its length by normal stress that is applied.

• Pressure Stress  -  Stresses induced in vessels containing pressurized materials.

• Radial Stress  -  The stress towards or away from the central axis of a curved member.

• Residual Stress  -  Stresses caused by manufacturing processes in a solid material after the origional cause has been removed.

• Shear Stress (Tangential Stress)  -  Tends to deform the material by breaking rather than stretching without changing the volume by restraining the object.

• Structural Stress  -  Stresses produced in structural members because of the weight they support.

• Tensile Stress  -  A stress in which the two sections of material on either side of a stress plane tend to pull apart or elongate.

• Thermal Stress  -  Whenever temperature gradients are present in a material.

 

stress formula
\(\large{ \sigma = \frac{F}{A_c} }\)
Symbol	English	Metric
\(\large{ \sigma }\)  (Greek symbol sigma) = stress	\(\large{\frac{lbf}{in^2}}\)	\(\large{Pa}\)
\(\large{ A_c }\) = area cross-section	\(\large{ ft^2}\)	\(\large{ m^2}\)
\(\large{ F }\) = force	\(\large{ lbf }\)	\(\large{N}\)