Skip to main content

Moment of Inertia of a Sphere

 

Moment of Inertia of a Sphere Formula, Solid Sphere
\( I \;=\; \dfrac{2}{5} \cdot m \cdot r^2  \) 
Symbol English Metric
\(\large{ I }\) = Moment of Inertia \(lbm\;/\;ft^2-sec\) \(kg\;/\;m^2\)
\(\large{ m }\) = Mass \( lbm \) \( kg \)
\(\large{ r }\) = Radius \( in \) \( mm \)

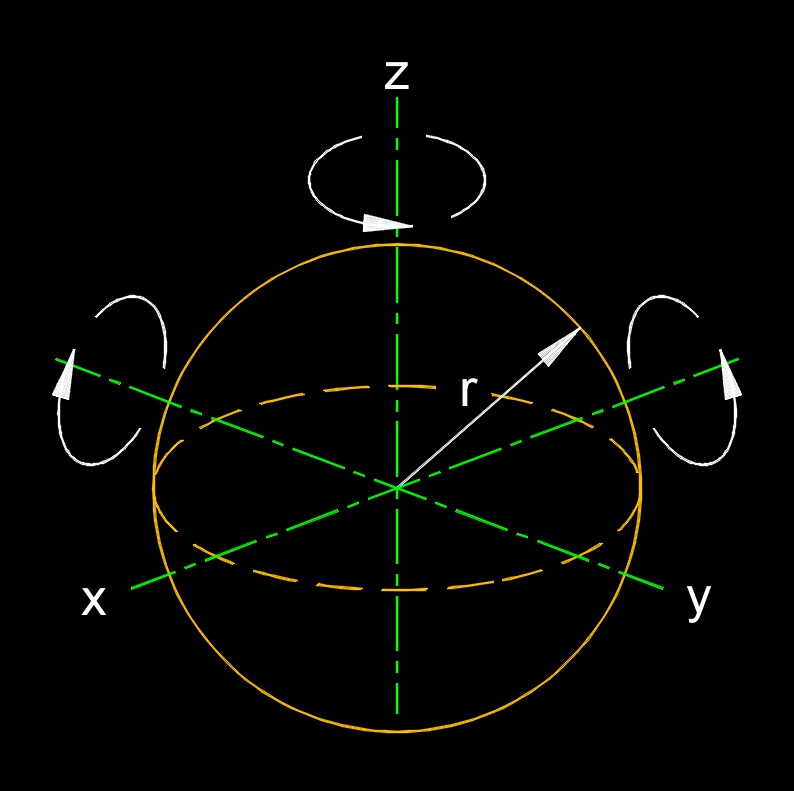
moment of inertia Sphere solid 1Piping Designer Logo 1

Moment of Inertia of a Sphere Formula, Hollow Sphere
\( I \;=\; \dfrac {2}{3} \cdot m \cdot r^2 \) 
Symbol English Metric
\(\large{ I }\) = Moment of Inertia \(lbm\;/\;ft^2-sec\) \(kg\;/\;m^2\)
\(\large{ m }\) = Mass \( lbm \) \( kg \)
\(\large{ r }\) = Radius \( in \) \( mm \)

moment of inertia Sphere solid 1  

 

 

 

 

 

 

 

 

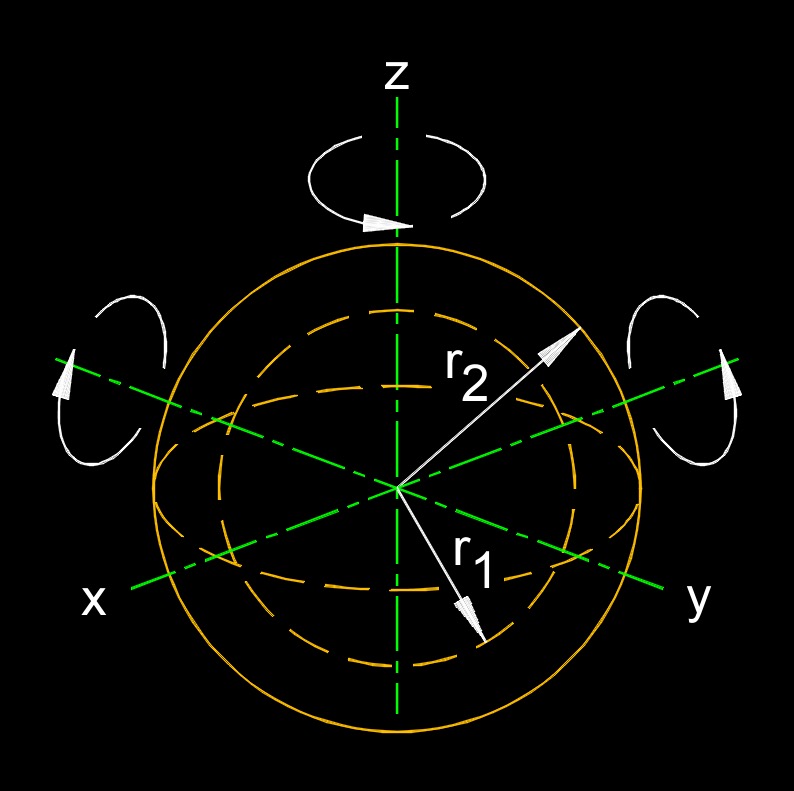
Moment of Inertia of a Sphere Formula, Hollow Core Sphere
\( I \;=\; \dfrac{2}{5} \cdot m \cdot r^2 \cdot \dfrac{ r_2^5 - r_1^5 }{ r_2^3 - r_1^3 } \) 
Symbol English Metric
\(\large{ I }\) = Moment of Inertia \(lbm\;/\;ft^2-sec\) \(kg\;/\;m^2\)
\(\large{ m }\) = Mass \( lbm \) \( kg \)
\(\large{ r }\) = Radius \( in \) \( mm \)
\(\large{ r_1 }\) = Radius \( in \) \( mm \)
\(\large{ r_2 }\) = Radius \( in \) \( mm \)

moment of inertia Sphere hollow 1