Moment of Inertia of a Circle
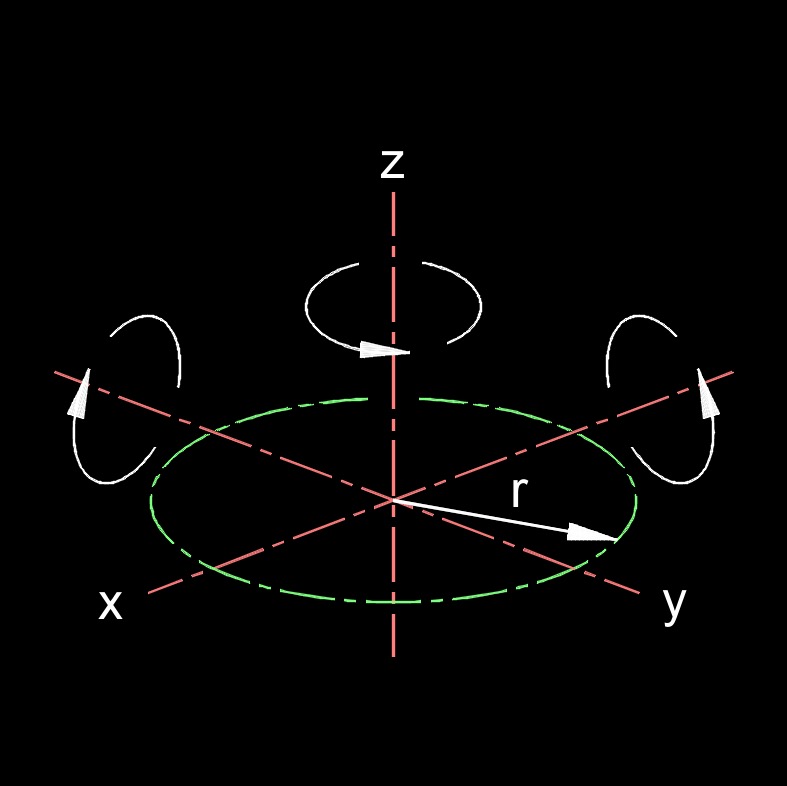The moment of inertia of a circle, also known as the rotational inertia, depends on the mass distribution within the circle and its axis of rotation. The formula assumes that the axis of rotation is perpendicular to the plane of the circle and passes through its center. If the axis of rotation is different or the mass distribution within the circle is not uniform, the moment of inertia will have a different value.
Moment of Inertia of a Circle formula, Hollow Plane |
||
|
\( I_z \;=\; m \; r^2 \) (Moment of Inertia of a Circle, Hollow Plane) \( m \;=\; Iz \;/\; r^2 \) \( r \;=\; \sqrt{ Iz \;/\; m } \) |
||
| Symbol | English | Metric |
| \( I \) = Moment of Inertia | \(lbm \;/\; ft^2-sec\) | \(kg \;/\; m^2\) |
| \( m \) = Mass | \( lbm \) | \( kg \) |
| \( r \) = Radius | \( in \) | \( mm \) |
Moment of Inertia of a Circle formulas, Solid Plane |
||
|
\( I_z \;=\; \frac{1}{2}\; m \; r^2 \) \( I_z \;=\; \frac{1}{2}\; \pi \; r^4 \) \( I_x \;=\; I_y \;=\; \frac{1}{4} \;m \; r^4 \) \( I_x \;=\; I_y \;=\; \frac{1}{4}\; \pi \; r^4 \) \( I_x \;=\; I_y \;=\; \frac{1}{64}\; d^4 \) |
||
| Symbol | English | Metric |
| \( I \) = Moment of Inertia | \(lbm \;/\; ft^2-sec\) | \(kg \;/\; m^2\) |
| \( d \) = Diameter | \( in \) | \( mm \) |
| \( m \) = Mass | \( lbm \) | \( kg \) |
| \( \pi \) = Pi | \(dimensionless\) | \(dimensionless\) |
| \( r \) = Radius | \( in \) | \( mm \) |
Tags: Moment of Inertia Circle