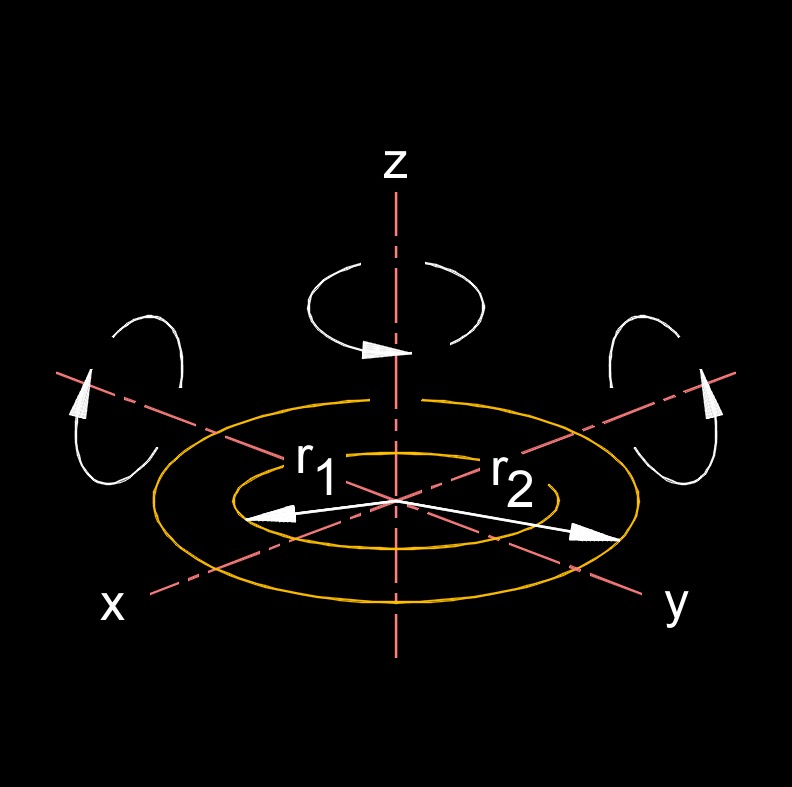
Moment of Inertia of an Annulus Formulas, Solid Plane
|
||
|
\( I_z \;=\; \dfrac {\pi}{2} \cdot \left( r_2{^4} - r_1{^4} \right) \) \( I_x \;=\; I_y \;=\; \dfrac {\pi}{4} \cdot \left( r_2{^4} - r_1{^4} \right) \) \( I_x \;=\; I_y \;=\; \dfrac {\pi}{64}\cdot D^4 - \dfrac {\pi}{64} \cdot d^4 \) |
||
| Symbol | English | Metric |
| \( I \) = Moment of Inertia | \(lbm\;/\;ft^2-sec\) | \(kg\;/\;m^2\) |
| \( d \) = Inside Diameter | \( in \) | \( mm \) |
| \( D \) = Outside Diameter | \( in \) | \( mm \) |
| \( \pi \) = Pi | \(dimensionless\) | \(dimensionless\) |
| \( r_1 \) = Radius | \( in \) | \( mm \) |
| \( r_2 \) = Radius | \( in \) | \( mm \) |
