Relative Roughness

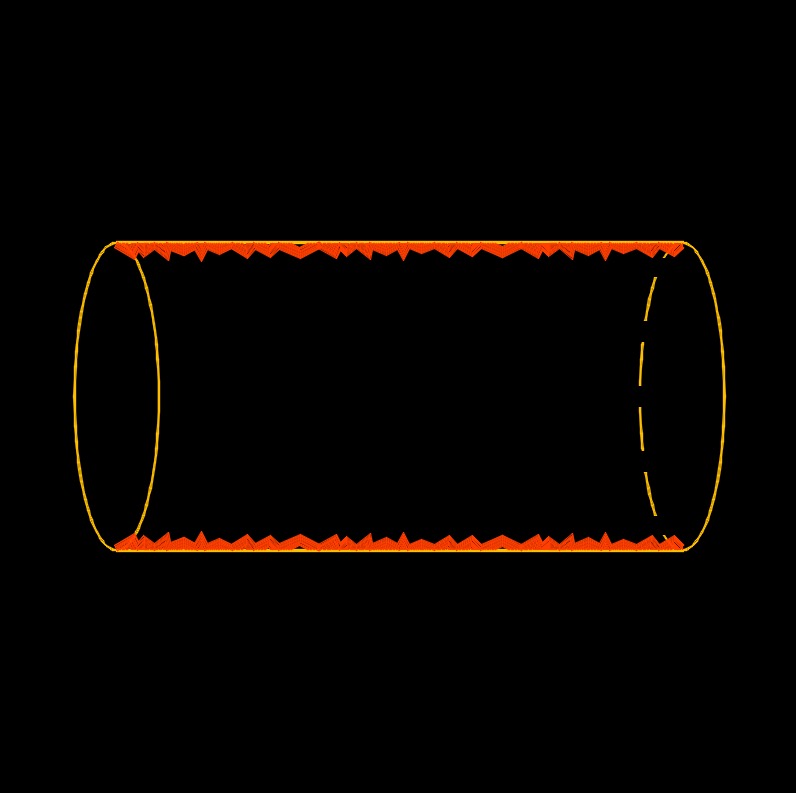Relative roughness, abbreviated as k, also known as the roughness coefficient or the hydraulic roughness , a dimensionless number, of a pipe is a ratio of the surface roughness to the diameter of the pipe.  Since the relative roughness is a dimensionless number, both the absolute roughness and diameter must carry the same units.  The relative roughness is used with the Moody Diagram when solving for the friction factor of a system.  The relative roughness provides a measure of the impact of surface roughness on fluid flow.  It affects the resistance to flow and pressure drop in a conduit.  In general, a higher relative roughness corresponds to a rougher surface, resulting in increased frictional losses and reduced flow capacity.

The relative roughness is an essential parameter in various flow calculations and equations, such as the Darcy-Weisbach equation, which is used to determine the head loss or pressure drop in pipes and channels.  It is commonly provided as a characteristic value for different types of conduits and materials to aid in the analysis and design of fluid flow systems.

 

Relative Roughness formula
\( k \;=\; \epsilon \;/\; d \)     (Relative Roughness) \( \epsilon \;=\; k \; d \) \( d \;=\; \epsilon \;/\; k \)
Symbol	English	Metric
\( k \) = Relative Roughness	\( dimensionless \)	\( dimensionless \)
\( \epsilon \)  (Greek symbol epsilon) = Absolute Roughness	\( in \)	\( mm \)
\( d \) = Pipe Inside Diameter	\( in \)	\( mm \)

 

Relative Roughness CALCULATOR