Inductance Formula |
||
|
\( L \;=\; \dfrac{ n^2 \cdot \mu \cdot A }{ l }\) (Inductance) \( n \;=\; \dfrac{ L \cdot l }{ 2 \cdot \mu \cdot A }\) \( \mu \;=\; \dfrac{ L \cdot l }{ n \cdot 2 \cdot A }\) \( A \;=\; \dfrac{ L \cdot l }{ n \cdot 2 \cdot \mu }\) \( l \;=\; \dfrac{ n^2 \cdot \mu \cdot A }{ L }\) |
||
| Symbol | English | Metric |
| \(\ L \) = Inductance | \(H\) | \(kg-m^2\;/\;s^2-A^2\) |
| \( n \) = Number of Turns of the Coil | \(dimensionless\) | \(dimensionless\) |
| \( \mu \) (Greek symbol mu) = Permeability | \(ft\;/\;sec\) | \(m\;/\;s\) |
| \( A \) = Area Encircled by the Coil | \(in^2\) | \(mm^2\) |
| \( l \) = Coil Length | \(in\) | \(mm\) |
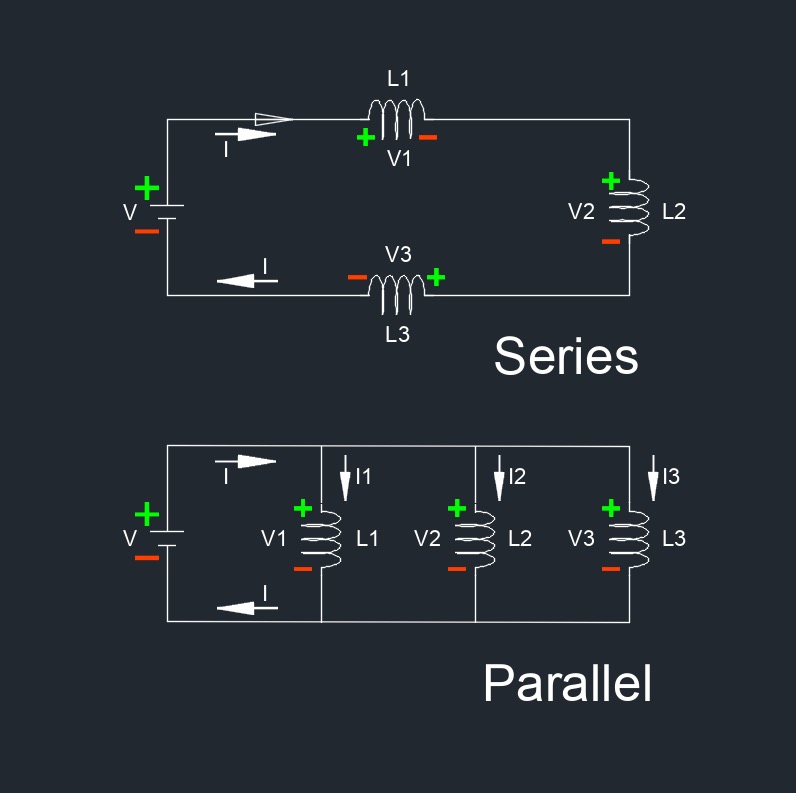Inductance, abbreviated as L, is a property of an electrical circuit or component that stores energy in a magnetic field when an electric current flows through it. Inductance is primarily associated with inductors, which are passive electronic components specifically designed to provide inductance. An inductor typically consists of a coil of wire wound around a core, which may be made of a magnetic material. When a current flows through the coil, a magnetic field is generated around it, and energy is stored in this magnetic field.
The inductance of an inductor depends on factors such as the number of turns in the coil, the size and shape of the coil, and the magnetic properties of the core material. It is directly proportional to the number of turns in the coil and the magnetic permeability of the core material.
Key Points about the Behavior of Inductance in a Circuit
Inductors oppose changes in current - According to Faraday's law of induction, when the current through an inductor changes, it induces an electromotive force (EMF) that opposes the change. This property is responsible for inductors' tendency to resist changes in current flow and their ability to store energy.
Inductors store energy in a magnetic field - When current flows through an inductor, energy is stored in the magnetic field associated with the inductor. This energy can be released back into the circuit when the current through the inductor changes.
Inductance affects the rate of change of current - Inductance influences the rate at which the current through an inductor can change. Higher inductance values result in slower changes in current, while lower inductance values allow for faster changes.
Inductors and inductance are important in various applications, including power supplies, filters, signal conditioning circuits, transformers, and electric motors. They can be used to control current levels, filter out unwanted frequencies, and store energy temporarily. Additionally, inductance plays a significant role in electromagnetic compatibility (EMC) and electromagnetic interference (EMI) mitigation.
