Archimedes Principle
Archimedes Principle Formula |
||
|
\( B \;=\; \rho \cdot g \cdot V \) (Archimedes Principle) \( \rho \;=\; \dfrac{B }{ g \cdot V }\) \( V \;= \dfrac{ B }{ \rho \cdot g } \) |
||
| Symbol | English | Metric |
| \( B \) = Buoyancy | \(lbf\) | \(N\) |
| \( \rho \) (Greek symbol rho) = Fluid Density | \(lbm \;/\; ft^3\) | \(kg \;/\; m^3\) |
| \( g \) = Gravitational Constant | \(lbf-ft^2 \;/\; lbm^2\) | \(N -m^2 \;/\; kg^2\) |
| \( V \) = Soilds Volume | \(ft^3\) | \(m^3\) |
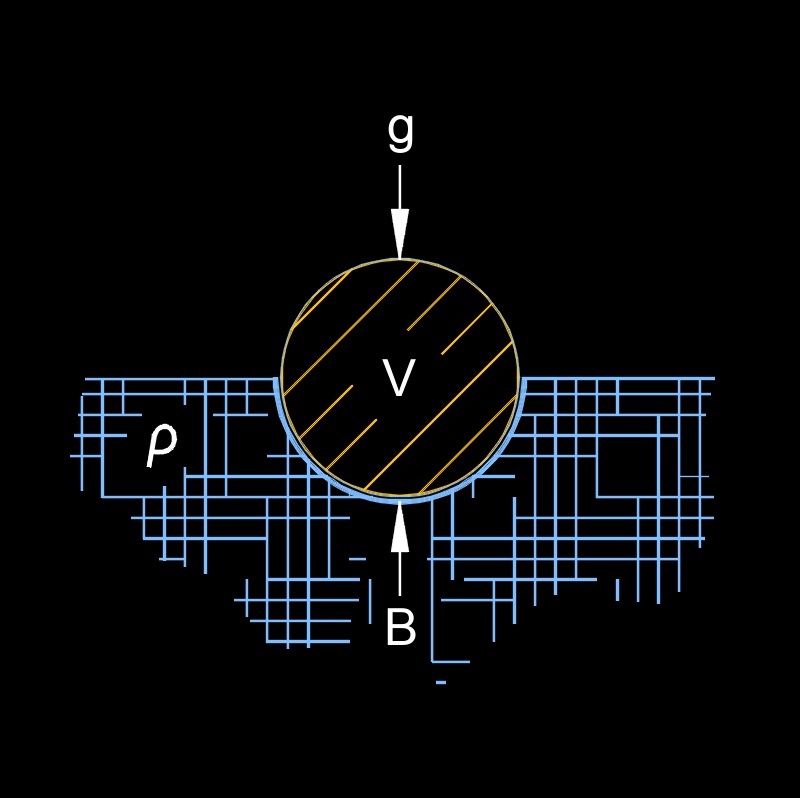
Archimedes principle is the upward bouyancy force that is extended on a body that is completely or partially immersed in a fluid and is equal to the weight of the fluid that the body displaces.
The Archimedes' principle, formulated by the ancient Greek mathematician and physicist Archimedes, states that when an object is immersed in a fluid (liquid or gas), it experiences an upward buoyant force that is equal to the weight of the fluid displaced by the object. In simpler terms, the principle explains why objects appear to weigh less when submerged in a fluid compared to when they are in air.
The buoyant force acting on an object is determined by the volume of fluid displaced by the object and the density of the fluid. The density of an object relative to the density of the fluid determines whether the object will float, sink, or remain suspended in the fluid.
This principle is particularly applicable to objects submerged in liquids, such as a ship floating in water or a balloon filled with gas in the air. It explains why objects with lower density than the fluid they are in float, while objects with higher density sink. It is also the basis for various applications, such as determining the buoyancy of boats and designing submarines, as well as understanding the behavior of objects in fluids in fields like hydrodynamics and aerodynamics.

