Center of Mass for Two Masses Formula |
||
|
\( x_{cm} \;=\; \dfrac{m_1 \cdot x_1 + m_2 \cdot x_2}{m_1 + m_2} \) (Two Masses) \( x_{cm} \;=\; \dfrac{m_1 \cdot x_1 + m_2 \cdot x_2 + \cdots }{ m_1 + m_2 + \cdots }\) (Multiple Masses) |
||
| Symbol | English | Metric |
| \( x_{cm} \) = Center of Mass | \( ft \) | \(m\) |
| \( m_1 \) = Mass 1 | \( lbm \) | \( kg \) |
| \( m_2 \) = Mass 2 | \( lbm \) | \( kg \) |
| \( x_1 \) = Position 1 | \( ft \) | \(m\) |
| \( x_2 \) = Position 2 | \( ft \) | \(m\) |
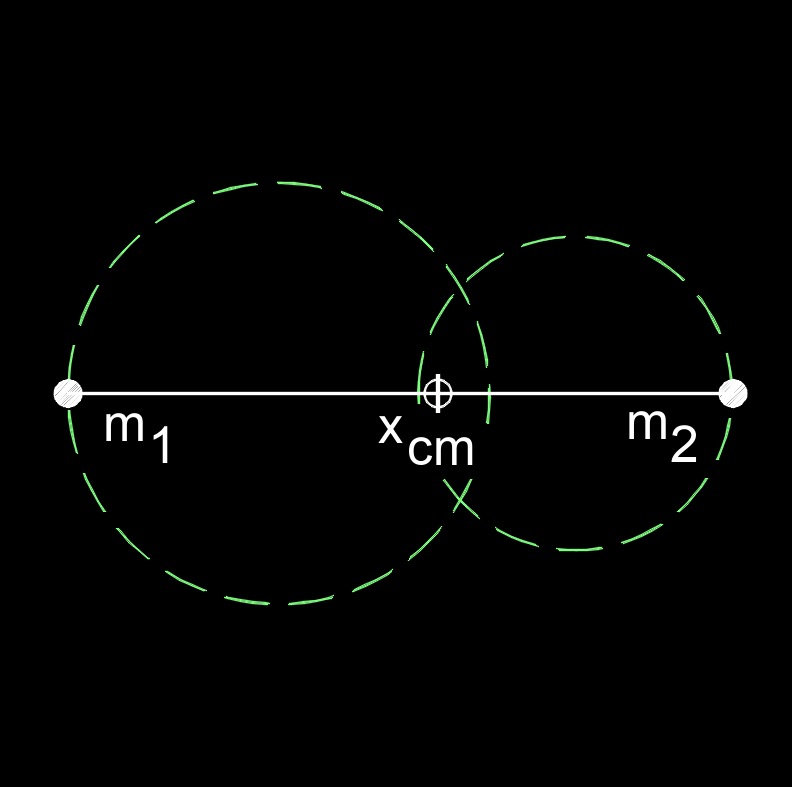Center of mass, abbreviated as COM, also called center of gravity, in a uniform gravitational field, is a concept in physics that describes the average position of the mass of an object. It is a point where the entire mass of an object can be considered to be concentrated for the purposes of analyzing its motion and behavior under the influence of external forces, such as gravity.
In other words, the center of mass is the point at which an object would balance perfectly if you were to support it. For symmetric objects with uniform density, the center of mass often coincides with the geometric center or the midpoint of the object. However, for irregularly shaped objects or those with non-uniform density, the center of mass may be located at a different point within the object.
In practical applications, finding the center of mass is essential for understanding the behavior of objects in various situations, such as analyzing the motion of a rocket, determining the stability of structures, or studying the orbits of celestial bodies.
Center of Mass Multiple Masses Formula
|
||
| \( x_{cm} \;=\; \dfrac{m_1 \cdot x_1 + m_2 \cdot x_2 + \cdots }{ m_1 + m_2 + \cdots }\) | ||
| Symbol | English | Metric |
| \( x_{cm} \) = Center of Mass | \( ft \) | \(m\) |
| \( m_1 \) = Mass 1 | \( lbm \) | \( kg \) |
| \( m_2 \) = Mass 2 | \( lbm \) | \( kg \) |
| \( x_1 \) = Position 1 | \( ft \) | \(m\) |
| \( x_2 \) = Position 2 | \( ft \) | \(m\) |