Heat Capacity Formula |
||
|
\( C \;=\; \dfrac{ \Delta Q }{ \Delta T }\) (Heat Capacity) \( \Delta Q \;=\; C \cdot \Delta T \) \( \Delta T \;=\; \dfrac{ \Delta Q }{ C }\) |
||
| Symbol | English | Metric |
| \( C \) = Heat Capacity | \(Btu\;/\;F\) | \(kJ\;/\;K\) |
| \( \Delta Q \) = Heat Transfered Amount | \(Btu\;/\;hr\) | \( W \) |
| \( \Delta T \) = Temperature Differential | \( F \) | \( K \) |
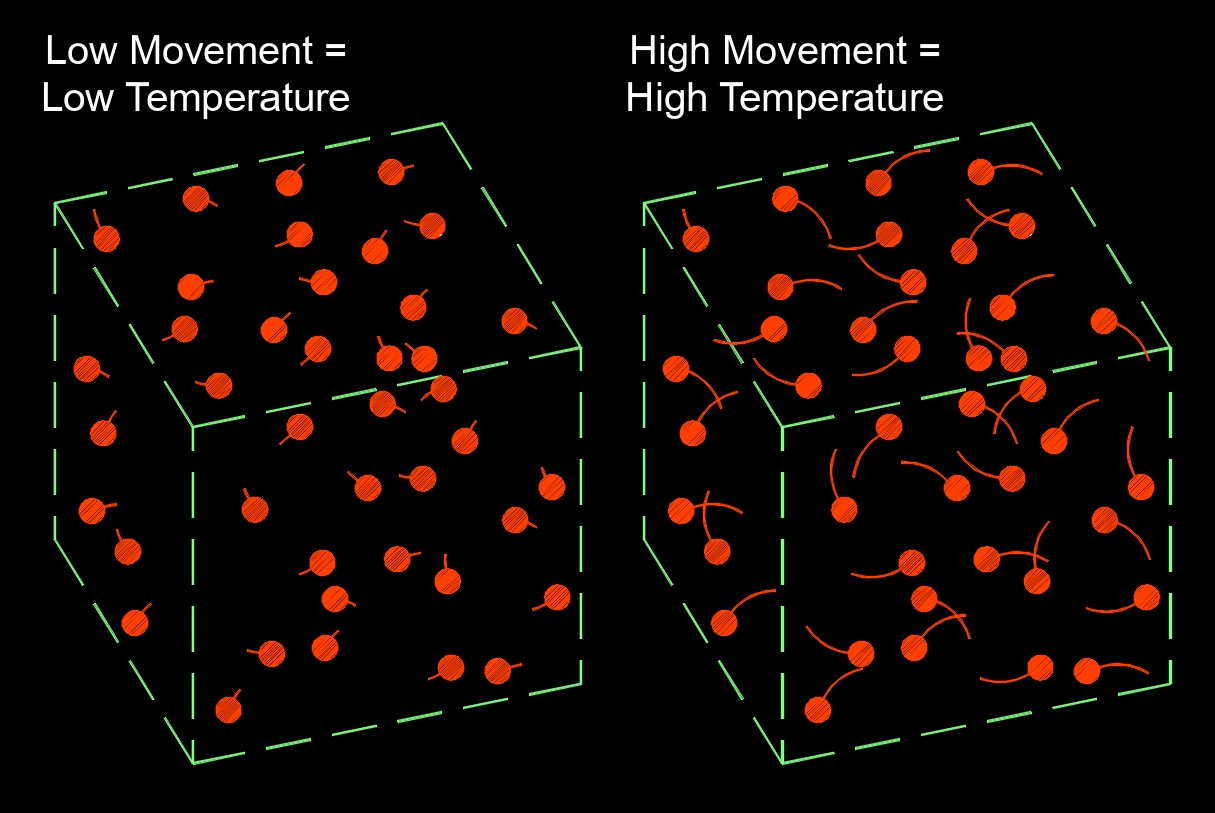Heat capacity, abbreviated as C or \(c_p\), is the amount of enerigy required to increase the temperature of a substance by 1°C. The heat gain or loss results in a change in temperature and the state and performance of work. The heat capacity of a substance is an important property in thermodynamics as it helps to determine the amount of energy needed to heat or cool a substance or system. It also influences the rate at which a substance changes temperature in response to thermal energy transfer.
Different substances and systems have different heat capacities due to variations in their molecular structure and composition. The heat capacity of a substance may also vary with temperature, particularly for materials that undergo phase transitions or exhibit other complex thermal behavior.
