Ideal Gas Law Pressure Formula |
||
|
\( p \;=\; \dfrac{ n \cdot R \cdot T }{ V }\) (Ideal Gas Law Pressure) \( n \;=\; \dfrac{ p \cdot V }{ R \cdot T }\) \( R \;=\; \dfrac{ p \cdot V }{ n \cdot T }\) \( T \;=\; \dfrac{ p \cdot V }{ n \cdot R }\) \( V \;=\; \dfrac{ n \cdot R \cdot T }{ p }\) |
||
| Symbol | English | Metric |
| \( p \) = Gas Pressure | \(lbf\;/\;in^2\) | \(Pa\) |
| \( n \) = Number of Moles of Gas | \(dimensionless\) | \(dimensionless\) |
| \( R \) = Specific Gas Constant (Gas Constant) | \(ft-lbf\;/\;lbm-R\) | \(J\;/\;kg-K\) |
| \( T \) = Gas Temperature | \( R \) | \( K \) |
| \( V \) = Gas Volume | \( in^3 \) | \( mm^3 \) |
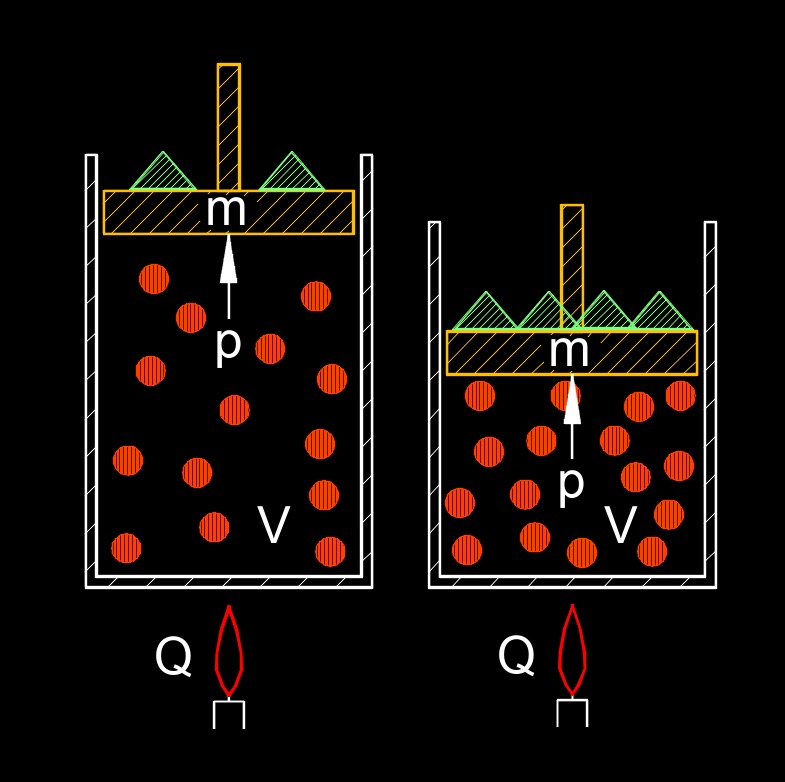The ideal gas law, expressed as PV=nRT. When we focus on pressure, this form highlights that the pressure exerted by an ideal gas is directly proportional to the amount of gas (number of moles) and its absolute temperature, while being inversely proportional to the volume it occupies. In essence, more gas in the same volume at the same temperature will lead to higher pressure due to more frequent collisions with the container walls. Similarly, increasing the temperature, which increases the kinetic energy of the gas molecules, results in greater pressure. Conversely, expanding the volume allows the gas molecules to spread out, leading to fewer collisions per unit area and thus a lower pressure.
