Skip to main content

Electromotive Force

 

Electromotive Force Formula

  • Energy and Charge

\( \epsilon \;=\;  \dfrac{ W }{  Q  }\)     (Electromotive Force)

\( W \;=\;  \epsilon \cdot  Q \)

\( Q \;=\;  \dfrac{ W }{  \epsilon  }\)
Symbol English Metric
\( \epsilon \)  (Greek symbol epsilon) = Electromotive Force \(V\) \(V\)
\( W \) = Work Done (Energy Supplied by the Source) \(J\) \(J\)
\( Q \) = Charge Moved \(C\) \(C\)

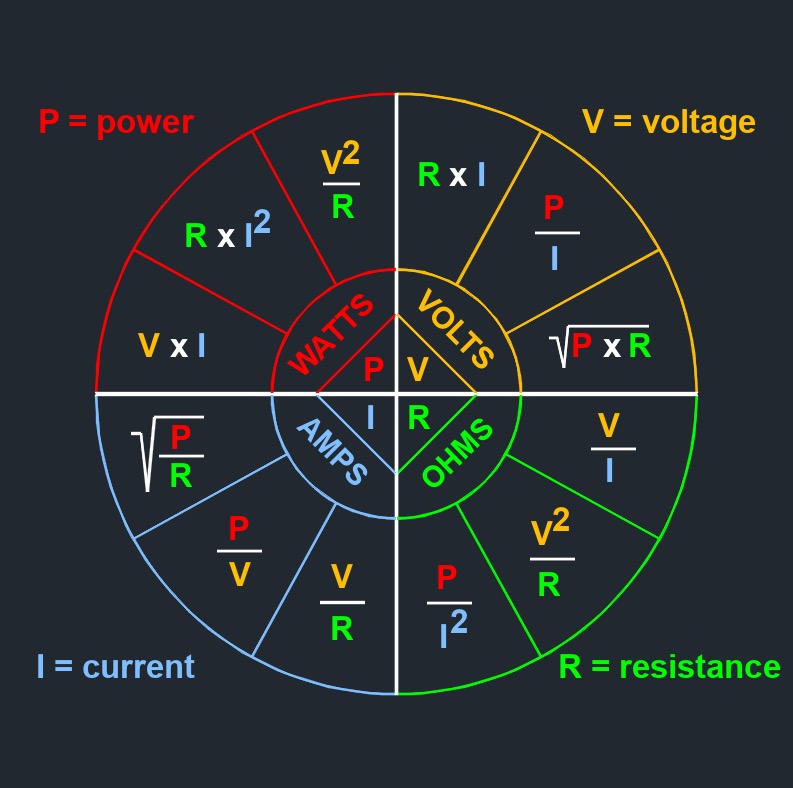pie chartElectromotive force, abbreviated as \(EMF\) or \( \epsilon \)  (Greek symbol epsilon), is the energy provided per unit charge by a source, such as a battery, generator, or other electrical device, that drives electric current through a circuit.  Despite its name, it is not an actual force but rather a potential difference measured in volts.  EMF represents the work done by the source to move a unit charge from the low-potential side to the high-potential side of the device, overcoming internal resistance and other energy losses.  EMF can be thought of as the voltage a source would supply if no current were flowing, making it the maximum potential available to drive charges.  EMF is needed to understand how electrical circuits operate, as EMF is what initiates and sustains the flow of electrons.

Electromotive Force Formula

  • Source with Internal Resistance

\( \epsilon \;=\;  I \cdot (R + r)  \)     (Electromotive Force)

\( I \;=\;  \dfrac{ \epsilon  }{ R + r  } \)

\( R \;=\;  \dfrac{ \epsilon }{ I } - r \)

\( r \;=\;  \dfrac{ \epsilon }{ I } - R \)
Symbol English Metric
\( \epsilon \)  (Greek symbol epsilon) = Electromotive Force \(V\) \(V\)
\( I \) = Current \(A\) \(A\)
\( R \) = External Resistance \(\Omega\) \(\Omega\)
\( r \) = Internal Resistance of the Source \(\Omega\) \(\Omega\)

Piping Designer Logo 1 

 

 

 

 

 

 

 

 

 

 

 

 

 

Electromotive Force Formula
\( \epsilon \;=\; -\; \dfrac{ \Phi_B }{  dt  }\)
Symbol English Metric
\( \epsilon \)  (Greek symbol epsilon) = Electromotive Force \(V\) \(V\)
\( \Phi_B \)  (Greek symbol Phi) = Magnetic Flux \(Wb\) \(Wb\)
\( \dfrac{ \Phi_B }{ dt }  \) = Rate of Change of Magnetic Flux \(Wb \;/\; sec\) \(Wb \;/\; s\)