Law of Conservation of Mechanical Energy Formula |
||
|
\( PE_i + KE_i \;=\; PE_f + KE_f \) (Law of Conservation of Mechanical Energy) \( PE_i \;=\; PE_f + KE_f - KE_i \) \( KE_i \;=\; PE_f + KE_f - PE_i \) \( PE_f \;=\; PE_i + KE_i - KE_f \) \( KE_f \;=\; PE_i + KE_i - PE_f \) |
||
| Symbol | English | Metric |
| \( PE_i \) = Initial Potential Energy | \( lbf-ft \) | \(kg-m^2\;/\;s^2\) |
| \( KE_i \) = Initial Kinetic Energy | \( lbf-ft \) | \(kg-m^2\;/\;s^2\) |
| \( PE_f \) = Final Potential Energy | \( lbf-ft \) | \(kg-m^2\;/\;s^2\) |
| \( KE_f \) = Final Kinetic Energy | \( lbf-ft \) | \(kg-m^2\;/\;s^2\) |
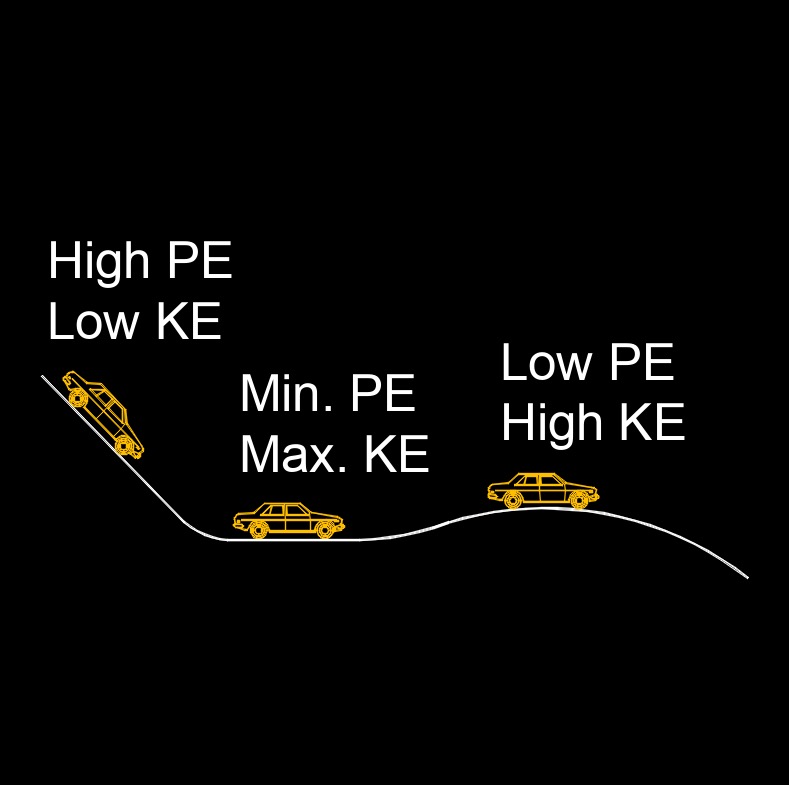Law of conservation of mechanical energy states the total mecanical energy in a system remains constant as long as the only force acting are conservative forces. In other words, the sum of the kinetic energy and potential energy within the system remains constant over time.
According to this law, if a system is not influenced by external forces like friction or air resistance, the total mechanical energy (KE + PE) remains constant. This means that the energy may transfer between kinetic and potential forms within the system, but the total amount remains unchanged.
It's important to note that this law assumes an idealized scenario without energy losses due to factors like non-conservative forces or thermal energy dissipation. In real world situations, mechanical energy conservation is often an approximation, and energy may be lost or transformed into other forms.
