Darcy Velocity or Flux Formula |
||
|
\( v \;=\; \dfrac{ v_s \cdot A_v }{ A_c }\) (Darcy Velocity) \( v_s \;=\; \dfrac{ v \cdot A_c }{ A_v }\) \( A_v \;=\; \dfrac{ v \cdot A_c }{ v_s }\) \( A_c \;=\; \dfrac{ v_s \cdot A_v }{ v }\) |
||
| Symbol | English | Metric |
| \( v \) = Darcy velocity or flux | \(ft \;/\; sec\) | \(m \;/\; s\) |
| \( v_s \) = Seepage Velocity | \(ft \;/\; sec\) | \(m \;/\;s\) |
| \( A_v \) = Area Cross-section Voids | \(ft^2\) | \(m^2\) |
| \( A_c \) = Flow Area Cross-section | \(ft^2\) | \(m^2\) |
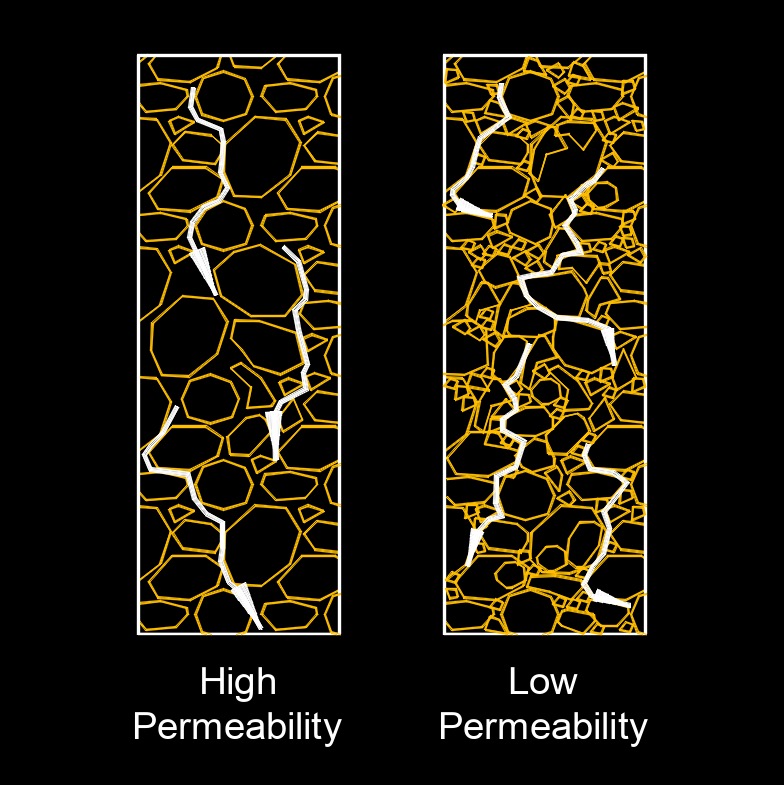Darcy velocity, abbreviated as v, also called Darcy's velocity or Darcy flux, is a term used in the field of fluid dynamics and porous media to describe the velocity of fluid flow through a porous medium, such as soil, rock, or a packed bed. Darcy velocity is defined as the volume of fluid (typically water) flowing through a cross-sectional area of the porous medium per unit of time.
Darcy's law, which is the foundation of Darcy velocity, describes the relationship between the flow rate of a fluid through a porous medium, the hydraulic conductivity of the medium, and the hydraulic head difference. It is an important concept in fields such as hydrogeology, soil mechanics, and groundwater flow modeling, as it helps to understand and predict fluid flow in porous materials.
Darcy Velocity or Flux Formula |
||
|
\( v \;=\; k \cdot i \) (Darcy Velocity) \( k \;=\; \dfrac{ v }{ i }\) \( i \;=\; \dfrac{ v }{ k }\) |
||
| Symbol | English | Metric |
| \( v \) = Darcy velocity or flux | \(ft \;/\; sec\) | \(m \;/\; s\) |
| \( k \) = Hydraulic Conductivity | \(ft \;/\; day\) | \(m \;/\; day\) |
| \( i \) = Hydraulic Gradient | \(dimensionless\) | \(dimensionless\) |
Darcy Velocity or Flux Formula |
||
|
\( v \;=\; v_s \cdot n \) (Darcy Velocity) \( v_s \;=\; \dfrac{ v }{ n }\) \( n \;=\; \dfrac{ v }{ v_s }\) |
||
| Symbol | English | Metric |
| \( v \) = Darcy velocity or flux | \(ft \;/\; sec\) | \(m \;/\;s\) |
| \( v_s \) = Seepage Velocity | \(ft \;/\; sec\) | \(m \;/\;s\) |
| \( n \) = Porosity | \(dimensionless\) | \(dimensionless\) |