Torricelli's Law

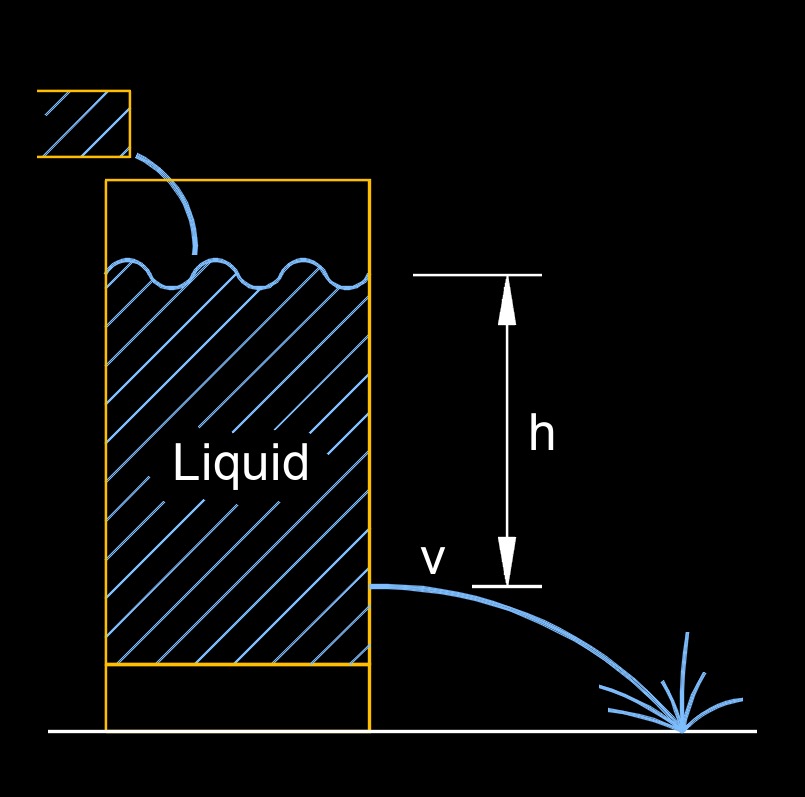
Torricelli's law, also called Torricelli's principle or Torricelli's theorem, is the fluid efflux velocity flowing through an orifice under gravity at the bottom of a tank filled to a depth.  This is the same velocity from the orifice as a falling body over the same height due to gravity.  Torricelli's law states that the velocity of a fluid flowing out of a small opening in a container, known as an orifice, is directly proportional to the square root of the height of the fluid above the opening.

In other words, Torricelli's law states that the velocity of fluid exiting an orifice is determined by the height of the fluid column above the orifice, and the acceleration due to gravity.  The law assumes that the fluid is incompressible and that there is no significant friction or energy losses during the flow.

This law has applications in various fields, including hydrodynamics, fluid dynamics, and engineering.  It helps in understanding the behavior of fluid flow through openings, such as in the case of water flowing out of a small hole in a container or a pipe.  The law is also relevant in calculating flow rates, designing fluid systems, and estimating the velocity of fluid discharges in practical situations.

 

Torricelli's law formula
\( v \;=\; \sqrt{ 2 \; g \; h }  \)     (Torricelli's Law) \( h \;=\; v^2 \;/\; 2 \; g  \)
Symbol	English	Metric
\( v \) = Velocity	\(ft\;/\;sec\)	\(m\;/\;s\)
\( g \) = Gravitational Acceleration	\(ft\;/\;sec^2\)	\(m\;/\;s^2\)
\( h \)  (Greek symbol rho) = height	\(ft\)	\(m\)