Shear Modulus
Shear Modulus Formula |
||
|
\( G \;=\; \dfrac{ \tau }{ \gamma }\) (Shear Modulus) \( \tau \;=\; G \cdot \gamma \) \( \gamma \;=\; \dfrac{\tau }{ G }\) |
||
| Symbol | English | Metric |
| \( G \) = Shear Modulus | \(lbf \;/\; in^2\) | \(Pa\) |
| \( \tau \) (Greek symbol tau) = Shear Stress | \(lbf \;/\; in^2\) | \(Pa\) |
| \( \gamma \) (Greek symbol gamma) = Shear Strain | \(deg\) | \(rad\) |
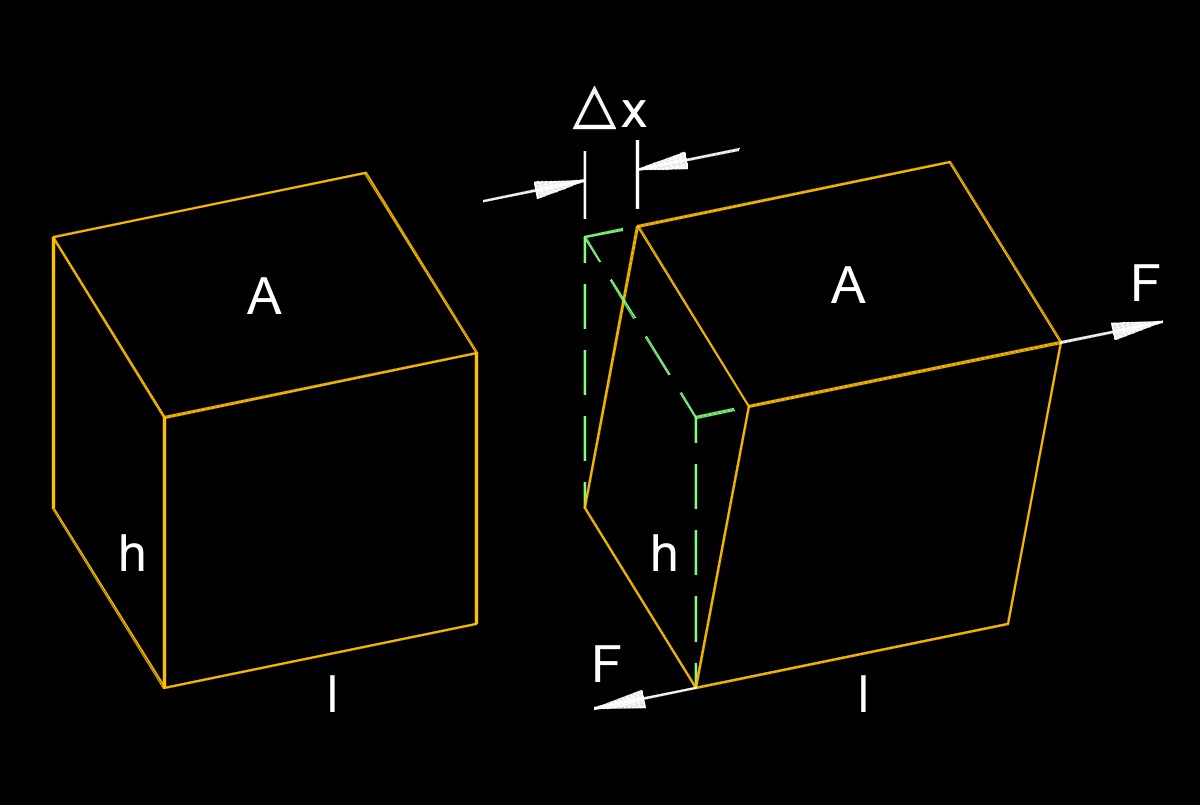 Shear modulus, abbreviated as \(G\), also called modulus of rigidity, elastic modulus for shear or shear modulus of elasticity, is a material property that describes its resistance to shear deformation when a shearing force is applied. Shearing force involves forces that act parallel to each other but in opposite directions, causing adjacent layers of a material to slide past each other. Shear modulus is one of the elastic moduli, alongside Young's modulus and bulk modulus, which describe a material's response to different types of deformation.
Shear modulus, abbreviated as \(G\), also called modulus of rigidity, elastic modulus for shear or shear modulus of elasticity, is a material property that describes its resistance to shear deformation when a shearing force is applied. Shearing force involves forces that act parallel to each other but in opposite directions, causing adjacent layers of a material to slide past each other. Shear modulus is one of the elastic moduli, alongside Young's modulus and bulk modulus, which describe a material's response to different types of deformation.
Shear modulus is an important material property in engineering and materials science because it helps determine a material's ability to withstand shearing forces and maintain its shape. Materials with high shear modulus values are stiffer and more resistant to shear deformation, while materials with low shear modulus values are more flexible and deform more easily under shear stress. The shear modulus is used in various engineering applications, including designing structures, analyzing the behavior of materials under load, and predicting the performance of mechanical components.

