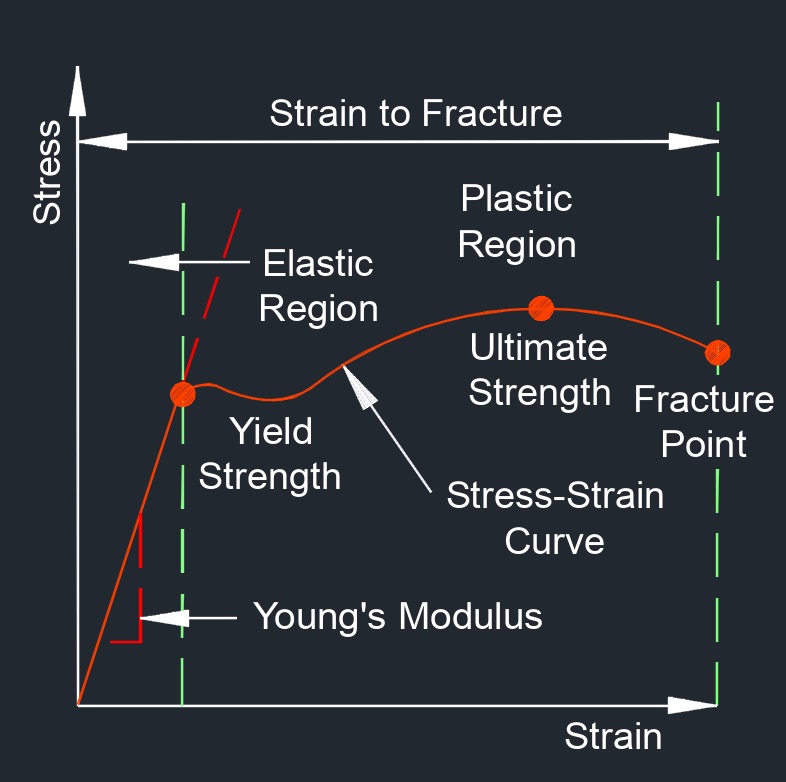
Young's Modulus
Young's Modulus Formula |
||
|
\( E \;=\; \dfrac{ \sigma }{ \epsilon }\) (Young's Modulus) \( \sigma \;=\; E \cdot \epsilon \) \( \epsilon \;=\; \dfrac{ \sigma }{ E }\) |
||
| Symbol | English | Metric |
| \( E \) = Young's Modulus | \(lbf\;/\;in^2\) | \(Pa\) |
| \( \sigma \) (Greek symbol sigma) = Stress | \(lbf\;/\;in^2\) | \(Pa\) |
| \( \epsilon \) (Greek symbol epsilon) = Strain | \(dimensionless\) | \(dimensionless\) |
Young's modulus, abbreviated as Yo or E, also called elastic modulus, modulus of elasticity, and tension modulus, is the measures the stiffness of an elastic material. The ratio of the longitudinal stress applied to a body or substance to the resulting longitudinal strain within the elastic limits. It represents the slope of the stress-strain curve within the elastic region of a material. The elastic region is the range of deformation where the material can return to its original shape and size after the stress is removed.
Young's Modulus Formula |
||
|
\( E \;=\; \dfrac{ F \cdot L_o }{ A_c \cdot \Delta_l }\) (Young's Modulus) \( F \;=\; \dfrac{ E \cdot A_c \cdot \Delta_l }{ L_o }\) \( L_o \;=\; \dfrac{ E \cdot A_c \cdot \Delta_l }{ F}\) \( A_c \;=\; \dfrac{ F \cdot L_o }{ E \cdot \Delta_l }\) \( \Delta_l \;=\; \dfrac{ F \cdot L_o }{ E \cdot A_c }\) |
||
| Symbol | English | Metric |
| \( E \) = Young's Modulus | \(lbf\;/\;in^2\) | \(Pa\) |
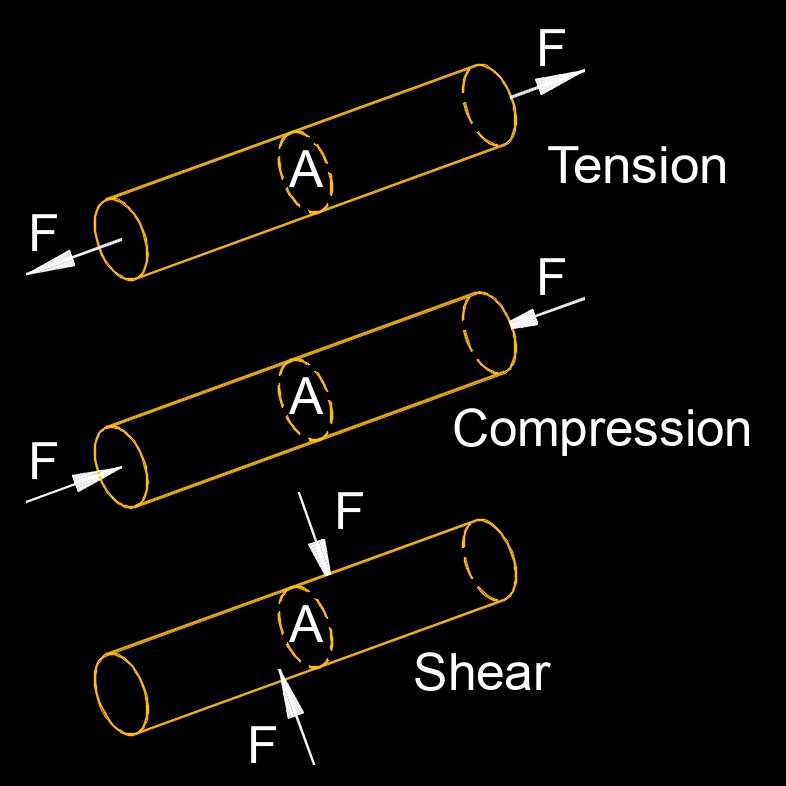
| \( F \) = Force Exerted on an Object Under Tension | \(lbf\) | \(N\) |
| \( L_o \) = Original Length of the Object | \(in\) | \(mm\) |
| \( A_c \) = Original Area Cross-section Through Which the Force is Applied | \(in^2\) | \(mm^2\) |
| \( \Delta_l \) = Change in Length of Object | \(in\) | \(mm\) |
Young's modulus is specific to each material and is influenced by factors such as the nature of the material's atomic structure, the type and strength of intermolecular or interatomic bonds, and the material's microstructure. It is widely used in engineering and materials science to assess the mechanical behavior and performance of materials under different loading conditions. Higher values of Young's modulus indicate stiffer materials that require greater stress to induce a given amount of strain, while lower values indicate more flexible or compliant materials. For example, steel has a high Young's modulus, indicating its stiffness, while rubber has a low Young's modulus, indicating its flexibility.