Stiffness
Stiffness Formula |
||
|
\( k \;=\; \dfrac{ F_a }{ d }\) (Stiffness) \( F_a \;=\; k \cdot d \) \( d \;=\; \dfrac{ F_a }{ k }\) |
||
| Symbol | English | Metric |
| \( k \) = Stiffness | \(lbf\;/\;in^2\) | \(Pa\) |
| \( F_a \) = Applied Force | \( lbf\) | \( N\) |
| \( d \) = Displacement | \( lbf \) | \(N\) |
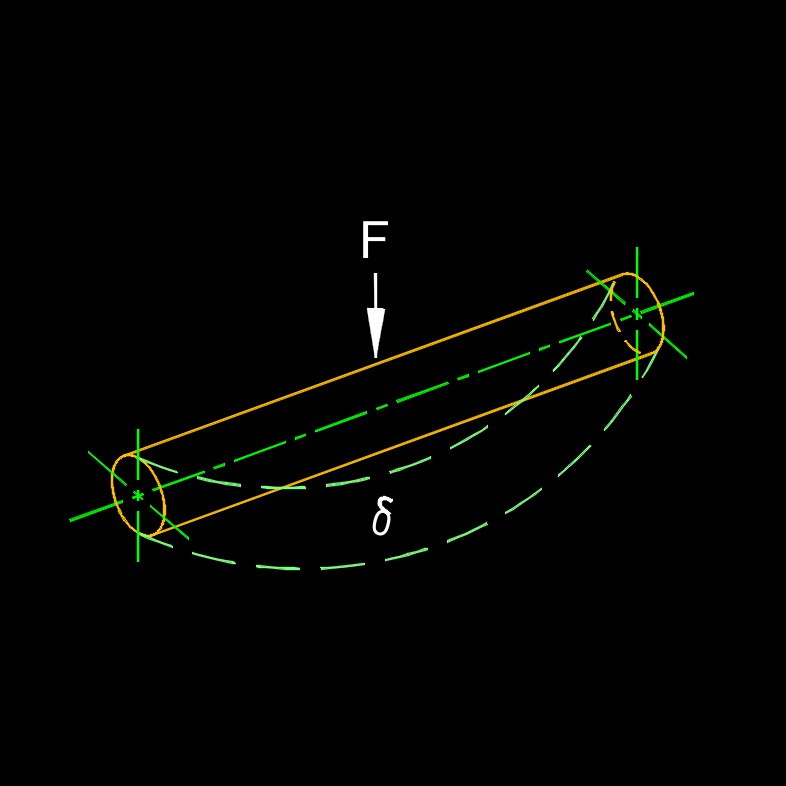 Stiffness, abbreviated as k, is the resistance of the elastic deformation of an object that applies to both compression and tension. It is a measure of how much a material or structure resists changes in shape or size in response to external loads or displacements. In simple terms, stiffness describes how rigid or flexible a material or structure is. A stiffer material or structure requires a larger force to produce a given deformation compared to a less stiff material or structure.
Stiffness, abbreviated as k, is the resistance of the elastic deformation of an object that applies to both compression and tension. It is a measure of how much a material or structure resists changes in shape or size in response to external loads or displacements. In simple terms, stiffness describes how rigid or flexible a material or structure is. A stiffer material or structure requires a larger force to produce a given deformation compared to a less stiff material or structure.
Stiffness is often quantified by the elastic modulus, also known as the modulus of elasticity or Young's modulus. The elastic modulus is a material property that measures the stiffness or rigidity of a material. It represents the ratio of stress to strain within the material's elastic range, as per Hooke's law. The higher the elastic modulus, the stiffer the material. For example, metals such as steel or titanium generally have high elastic moduli, indicating their high stiffness. In contrast, materials like rubber or foam have low elastic moduli, making them more flexible or compliant.
Stiffness is a crucial property in various engineering applications. In structural engineering, it determines the response of a structure to applied loads, affecting its stability, strength, and overall performance. Stiffness also plays a significant role in designing mechanical components, such as springs, beams, or frames, where controlling deflections or ensuring proper load distribution is essential. It is important to note that stiffness can vary depending on the direction of the applied force or deformation. Anisotropic materials, such as composites or wood, may exhibit different stiffness properties in different directions.

