Strain Length Change Formula |
||
|
\( \Delta L \;=\; \epsilon \cdot L_i \) (Strain Length Change) \( \epsilon \;=\; \dfrac{ \Delta L }{ L_i }\) \( L_i \;=\; \dfrac{ \Delta L }{ \epsilon }\) |
||
| Symbol | English | Metric |
| \( \Delta L \) = change in length | \( in \) | \( mm \) |
| \( \epsilon\) (Greek symbol epsilon) = strain | \( dimensionless \) | \( dimensionless \) |
| \( L_i \) = initial length | \( in \) | \( mm \) |
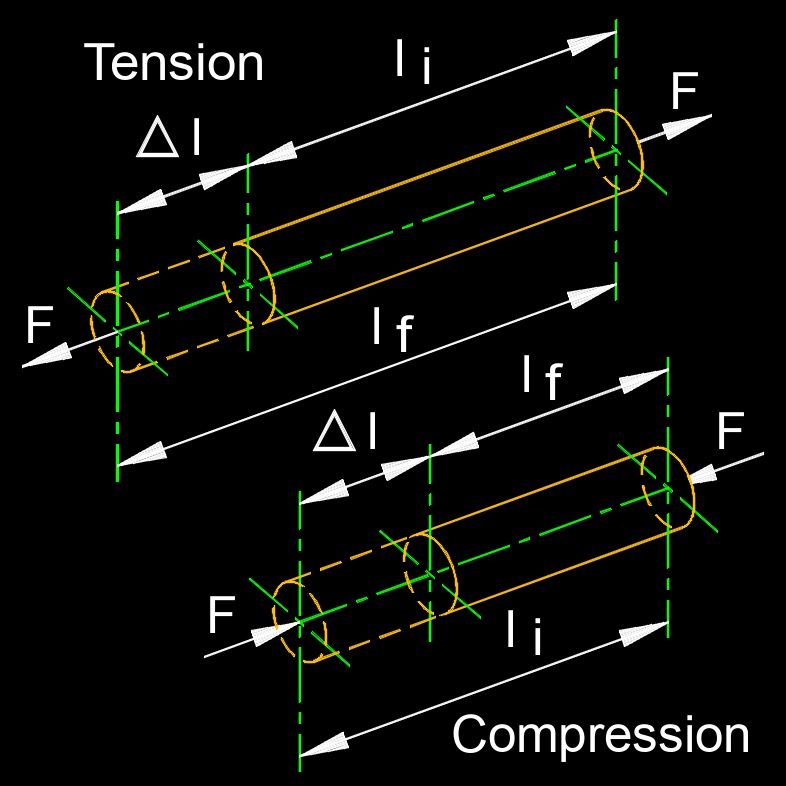Strain change length, abbreviated as \( \Delta L \), is the amount by which a material’s length changes when it is subjected to stress or deformation. It represents the actual elongation or contraction that occurs along the axis of the material due to applied forces. The change in length is directly proportional to the original length of the material and the amount of strain experienced, which is the ratio of the deformation to the original length. In materials that obey Hooke’s law, this change can also be expressed in terms of the applied stress divided by the material’s Young’s modulus, showing the relationship between the material’s stiffness and how much it stretches or compresses under load. Essentially, the strain change length quantifies the physical response of a material to mechanical loading.
