Fluid Pressure at Depth

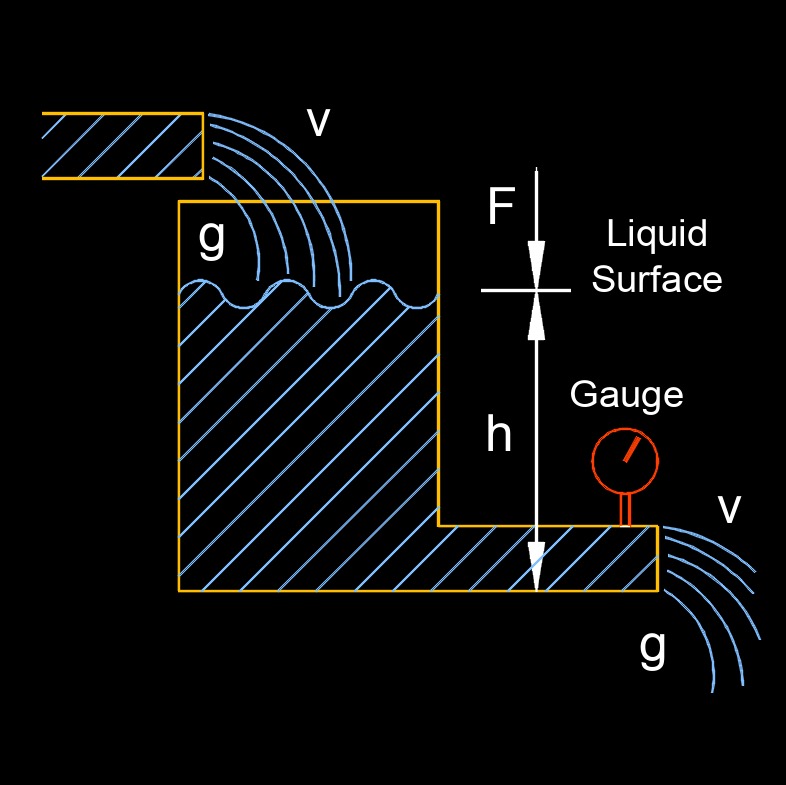Fluid pressure at a depth in a fluid column is determined by the weight of the overlying fluid.  This is described by Pascal's law, which states that a change in pressure applied to an enclosed fluid is transmitted undiminished to all portions of the fluid and to the walls of its container.

This formula is derived from the hydrostatic pressure equation, which states that the pressure at any point in a fluid at rest is the same in all directions and is equal to the weight of the fluid column above that point divided by the area.  As you descend deeper into a fluid, the pressure increases due to the increased weight of the fluid above pressing down on the fluid at lower levels.  The pressure increases linearly with depth.

 

Fluid PRESSURE at Depth formula
\( p =  \rho \;  g  \;  h  \)     (Fluid Pressure at Depth) \( \rho =   p \;/\; g \; h \) \( g =  p \;/\; \rho \; h \) \( h =   p \;/\; \rho \; g \)
Symbol	English	Metric
\( p \) = Fluid Pressure	\(lbf\;/\;in^2\)	\(Pa\)
\( \rho \)   (Greek symbol rho) = Density of Fluid	\(lbm\;/\;ft^3\)	\(kg\;/\;m^3\)
\( g \) = Gravitational Acceleration	\(ft\;/\;sec^2\)	\(m\;/\;s^2\)
\( h \) = Height of Depth of Fluid	\(ft\)	\(m\)